wykresy funkcji kwadratowej jamm: Narysuj wykres funkcji kwadratowej |x²−2x|−3 Chciałbym widzieć co tu po kolei zrobić najpierw X²−2x potem przesunięcie o wektor −3 i wartość bezwzgledna czy jak?

x: najpierw wartość bezwzględna, potem wektor v=[0,−3]

Jack: |x²−2x| = |x(x−2)| = |x| * |x−2| zrob 3 przedzialy i dla kazdego wyznacz jak to narysowac. 1) x ∊ (−∞;0> y = (−x) * (2−x) − 3 = x² − 2x − 3 2) x∊ (0;2> y = x * (2−x) − 3 = − x² + 2x − 3 3) x ∊ (2;∞) y = ... twoje zadanie to narysowac ten fragment paraboli w danym przedziale

jamm: ktos moglby mi to rozrysowac bo coś się pogubiłem wyszły mi miejsca zerowe −2 i 0 a p wyszło 1 i jakoś dziwne to

Janek191: Tutaj nie widzę żadnej funkcji ! f : D → P x → f(x)

jamm: f(x)=|x2−2x|−3

jamm: f(x) = |x²−2x|−3

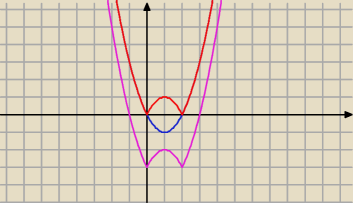
bezendu: Rysujesz f(x)=x²−2x (niebieska) Odbijasz to co jest pod osią OY nad oś (czerwona) Opuszczasz całą funkcję o wektor v=[0,−3] (różowa)

jamm: a czemu mi wyszło jedno miejsce zerowe −2 zamiast 2 jak chyba dobrze liczyłem

Adamm: właśnie źle, −2 nie mogło wyjść

Mila: Miejsca zerowe f(x): |x²−2x|−3=0⇔ |x²−2x|=3 x²−2x=3 lub x²−2x=−3 x²−2x−3=0 lub x²−2x+3=0 Δ=16 lub Δ=4−12<0 brak miejsc zerowych

	2−4		2+4
x=		=−1 lub x=		=3 tak jak na wykresie bezendu
	2		2

jamm: a przy wykresie f(x)=|x²−9|−2x jak by to wygladalo? Chodzi mi raczej o wytlumaczenie niz podanie rozwiazania na tacy bo mi nic z tego

bezendu: Tu już trzeba rozbić to na przypadki i rysować w przedziałach.

jamm: a dałbyś rade mi to możliwie najprostszym sposobem wytłumaczyć co i jak krok po kroku?

bezendu: Masz już wytłumaczone w Twoim nowym poście.

Jack: bys rysowal w przedzialach to by nie bylo problemu