ekstrema ekstrema: mam pytanie dotyczace ekstremow globalnych gdy wyliczam ekstrema lokalne to jak sprawdzic czy sa globalne? wiem ze liczy sie granice do +−∞, ale skad wiedziec ktora jest do maksiumum, a ktora do minimum? w rozwiazaniach mam raz to raz to

yht: ekstrema to minima i maksima minimum globalne to takie minimum, które jest najmniejsze z minimów załóżmy że minima wyszły −4, 8 i −7 najmniejsza liczba z powyższej trójki liczb to −7 dlatego minimum globalnym jest −7, zaś −4 oraz 8 to minima lokalne załóżmy że maksima wyszły −53, 40 i 32 największa z tej trójki liczb to liczba 40 dlatego maksimum globalnym jest 40, zaś −53 i 32 to maksima lokalne −−−−−−−−−−−−−−−−−−−−−−−−−−−− minimum globalne to najmniejsze z minimów (czyli najmniejsza wartość funkcji) maksimum globalne to największe z maksimów (czyli największa wartość funkcji) −−−−−−−−−−−−−−−−−−−−−−−−−−−−− jeśli funkcja ma tylko jedno minimum i tylko jedno maksimum, to są one globalne funkcja może mieć co najwyżej jedno minimum oraz co najwyżej jedno maksimum globalne może mieć nieskończenie wiele minimów/maksimów lokalnych

Adamm: porównać która jest najmniejsza wartość to minimum, więc wybierasz najmniejszą z twoich ekstremum największa to maksimum więc wybierasz największą czy są globalne sprawdzasz analizując funkcję

ekstrema: znam definicje i umiem wyliczyc ekstrema lokalne http://imgur.com/a/cJBiH chodzi mi o tego typu zadania, w jednym zadaniu maksimum globalne sprawdza sie do +∞, w innym do −∞

ekstrema: (w sensie granice) i pytanie, od czego to zalezy?

ekstrema: intuicyjnie myslalem ze maksimum po prostu do +∞, ale nie zawsze tak ejst

Janek191: Poczytaj definicje ekstremów

ekstrema: no znam, ale nie potrafie zastosowac do tego : /

Adamm: to może powiedz z którym masz problem

marek: ekstrema globalne, to nie są największe/najmniejsze z ekstremów lokalnych! Ekstrema globalne to największa/najmniejsza wartość funkcji. Jeśli gdzieś wartości funkcji dążą do nieskończoności, to nie ma wartości największych/najmniejszych.

Adamm: nigdy nie powiedziałem że są

yht: masz rację marek − pomyliłem się, przecież ekstrema to są x−sy a nie igreki! można wykasować moją wypowiedź, nie przemyślałem i za szybko napisałem

Janek191: Coś tu kręcicie

ekstrema: chyba juz rozumiem − najpierw licze wartosci tych minimum(najmniejszych) i maksimum lokalnych(największych), potem granice do +−∞ funkcji jesli ktoras granica jest mniejsza lub rowna tym ekstremom to wtedy nie sa one globalnymi dobrze mysle?

Adamm: nie, jakie ekstremum ma funkcja |x|? nie ma ale minimum ma

ekstrema: to jest strasznie schematyczne zadanie z tego co widze i chce je ogarnac bo moze jutro byc na egzaminie(reszte juz prawie ogarniam)

Adamm: to zależy

Adamm: no cóż z f(x) z której możesz obliczyć pochodną to rób tak jak mówisz

Janek191:

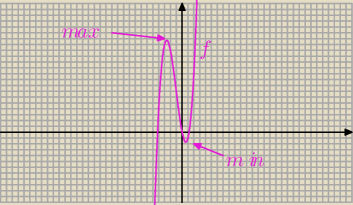
Janek191: Funkcja y = I x I ma minimum y_min = 0

ekstrema: wiem ogarniam to, umiem liczyc globlne jesli sa ograniczone przedzialem,ale w tym moim zadaniu chyba nie ma przedzialu

Adamm: Janek, właśnie to powiedziałem ale dzięki

ekstrema: dziedzina to R

ekstrema: lokalne se umiem wyliczyc, chodzi mi tylko o moment jak sprawdzic czy to sa globalne, czy dobrze napisalem 22;35

ekstrema: i przykladowe schematyczne zadanie 22;15

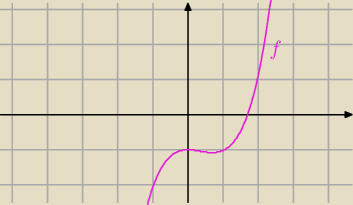
Janek191: f(x) = e^x −2 e^−x −3 x

Janek191: Funkcja ma maksimum lokalne i minimum lokalne Nie ma minimum globalnego i maksimum globalnego, bo lim f(x) = − ∞ x→ −∞ oraz lim f(x) = +∞ x→+∞

ekstrema: wpisalem se na wolframie, ale mi chodzi bardziej jak to zapisac

Adamm: co zapisać?

ekstrema: a co jakby nie byly do +−∞? wtedy tak jak pisalem wyzej?

ekstrema: tzn jakby granice nie rownaly sie +−∞

Janek191: Jeżeli y_max jest największą wartością funkcji w Df, to jest maksimum globalnym.

Adamm: daj przykład, nie będziemy rozmawiać o czymś co nie istnieje

Adamm: dobra, ja dam np. masz arctgx

	1
(arctgx)'=		>0
	x2+1

dlatego funkcja rośnie na ℛ ale lim x→∞ arctgx = π/2 a lim x→−∞ arctgx = −π/2

ekstrema: http://imgur.com/a/VT7eP

Adamm: jeśli dla x→±∞ nie ma granicy niewłaściwej to sprawdzaj w punktach nieciągłości, potem ekstrema lub inne

Janek191: Ta funkcja nie ma ekstremów.

Adamm: np. tu mamy lim x→∞ f(x) = 0 lim x→ −∞ f(x) = ∞ nie ma maksimum, szukasz minimum

ekstrema: ok dobra, trudno nam sie bedzie tak dogadac, zapytam wiec inaczej − co trzeba krok po kroku zrobic jak sie obliczy ekstrema lokalne, zeby sprawdzic czy sa globalne?

ekstrema: ogolnie w obojetnie jakim przykladzie

Adamm: jak mówiłem, oprócz liczenia pochodnej, znajdywania ekstremów lokalnych, liczenia granic z punktów nieciągłości, ±∞, + czasami się znajdzie taki przypadek jak |x|

Adamm: na |x| możesz podzielić zawsze na 2 więc to też nie jest problem

Janek191: Ekstremum lokalne jest globalnym ekstremum, jeżeli jest największą ( lub najmniejszą) wartością tej funkcji w jej dziedzinie Df.

ekstrema: no czyli tak jak mowilem, o to mi chodzilo dzieki