Figury na płaszczyźnie kartezjańskiej, długość wektora Filip: Witam, pomógłby ktoś? Oblicz długość wektora u gdy,: u = [−√2 − 1, √2 +1]

Adamm: u=√(−√2−1)²+(√2+1)²=√2(√2+1)²=√2|√2+1|=2+√2

Mila: |u|=√(−√2−1)²+(√2+1)²=√2+2√2+1+2+2√2+1=√6+4√2=√(2+√2)²=2+√2

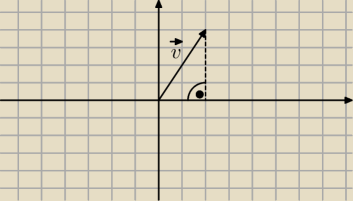
Benny: Jeśli v=[x,y] to jego długość wyraża się wzorem √x²+y², widać to np. z Twierdzenia Pitagorasa.

Filip: co oznacza √2|√2+1|, to moduły?

Adamm: tak, to moduł

Filip: Mila, wytłumacz mi skąd √6+4√2=√(2+√2)2

Eta: (2+√2)²= 4+4√2+2= 6+4√2

Mila: Trzeba zauważyć , że 4√2=2*2√2 i próbować zastosować wzór skróconego mnożenia : (a+b)²=a²+2a*b+b² a=2, b=√2 (2+√2)²=4+4√2+2=6+4√2 pasuje.