Pochodne
spring45: Pień o wysokości 6m ma kształt stożka ściętego, którego średnice podstaw są równe 1,2 m i 0,6
m. Z pnia tego należy wyciąć belkę o przekroju kwadratowym, która miałaby oś wspólną z osią
pnia i możliwie największą objętość. Oblicz wymiary tej belki.
5 wrz 20:05
Adamm:
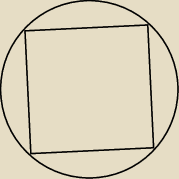
dla zmaksymalizowania kwadrat musi byc wewnątrz mniejszego promienia
mamy stąd prostopadłościan o wysokości 6m i przekątnej podstawy 0.6m
| | √2 | |
oznaczmy d=0,6m, √2a=0,6m, a= |
| m |
| | 10 | |
P=0,02m
2
V=0,012 m
3
5 wrz 20:58
Adamm: a, pytanie było o wymiary
5 wrz 21:00
Saizou :
Pytanie czy to będzie największa belka (w sensie objętości, bo pod względem długości owszem)?
5 wrz 21:02
Adamm: cytuję "która miałaby oś wspólną z osią pnia"
5 wrz 21:03
spring45: Dzięki
5 wrz 21:04
Saizou :
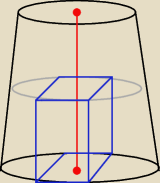

5 wrz 21:06
g:
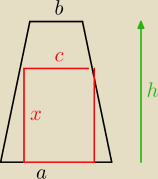
Największą objętość będzie miała belka o długości 4m.
| | 1 | | h | |
Trzeba znaleźć maksimum funkcji V(x). Maksimum jest dla x = |
| * |
| |
| | 3 | | 1−b/a | |
5 wrz 23:26
 dla zmaksymalizowania kwadrat musi byc wewnątrz mniejszego promienia
mamy stąd prostopadłościan o wysokości 6m i przekątnej podstawy 0.6m
dla zmaksymalizowania kwadrat musi byc wewnątrz mniejszego promienia
mamy stąd prostopadłościan o wysokości 6m i przekątnej podstawy 0.6m


 Największą objętość będzie miała belka o długości 4m.
Największą objętość będzie miała belka o długości 4m.