Finkcja homograficzna matthew: Funkcja homograficzna Cześć, mam taki przykład:

	x+2
f(x) =
	|2x−1|

Zrobiłem tak: 2x−1≠0

	1
x≠
	2

I x≥0

	5   4		1
y1 =		+
	1   x−   2		2

II x<0

	3   4		1
y2 =		−
	1   x+   2		2

W rysunku nie wiem co dalej zrobić.... Może ktoś sprawdzić mi ten przykład?

matthew: Ponawiam....

matthew: Ponawiam......

student:

	1		1		1
jak zauważyłeś dla x=		mianownik sie zeruje, natomiast dla x<		(x∊(−∞;		)
	2		2		2

	1
wyrażene pod wartością bezwzględną przyjmuje wartości ujemne, a dla x≥		dodatnie.
	2

zgodnie z definicją wartośxi bezwględnej:

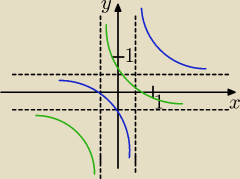
	1		x+2
dla x∊(−∞;		) f(x)=
	2		2x−1

	1		x+2
dla x∊<		;+∞) f(x)=
	2		−(2x−1)

student: na odwrót :

	1		x+2
dla x∊(−∞;		) f(x)=
	2		−(2x−1)

	1		x+2
dla x∊<		;+∞) f(x)=
	2		2x−1

matthew: Czyli będzie tak? I)

	1
x≥
	2

	x+2		1   +1 2		1   1   1   (x− ) +1 + 2   2   4
y =		=		=		=
	2x−1		x−{1}{2}		1   x−   2

	5   4		1
=		+
	1   x−   2		2

	5   4		1		1
y =		v = [		,		]
	x		2		2

II)

	1
x<
	2

	x+2		3   −   4		1
y =		=		−
	−(2x−1)		1   x+   2		2

matthew: A wiesz, jak zrobić takie zadanie? Dla jakiej wartości x funkcja homograficzna f przyjmuje podaną obok wartość?

	2x −5
f(x) =		, w = −5
	9x + 27

student: eee... nie tak to nie będzie ja nie jestem dobrym nauczycielem niestety. może ktoś się odważy wytłumaczyć Ci na czym to polega, ale to nie będę ja najlepiej idź do nauczyciela w szkole i zapytaj czy może Ci to wytłumaczyć w drugim zadaniu jeśli funkcja przyjmuje jakąś wartość oznacz to ze f(x) = w czyli u ciebie:

2x−5
	=−5 wystarczy rozwiazać
9x+27

student: znikam bo zaczyna mnie przytłaczać ilość wpadających na forum zadań

matthew: No ale dlaczego.... Przcież podałeś mi że:

	x+2		x+2
f(x) =		i f(x) =
	−(2x − 1)		2x − 1

ja tylko je rozwazałem, sprawdź mi to jeszcze raz... Dzięki za odpowiedzi

matthew: ponawiam...

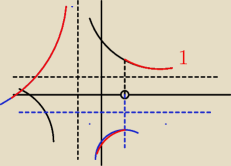ula: ja spróbuję nie możesz podstawiać pod x jakiejś liczby tylko obliczać funkcję zależną od x

	x+2
{		dla x∊(12; ∞)
	2x−1

f(x)=

	x+2
{		dla x∊(−∞;12)
	−2x+1

x+2
	=
2x−1

	(x−12)+72		x−12		7
		=		+		=
	2(x−12)		2(x−12)		4(x−12)

7
	+12
4(x−12)

z tego wyczytujemy, że podstawowy wykres przesuniety jest w lewo o ¹₂ i w górę o {1}{2} teraz 2 przypadek

(x−12)+72		−7
	=		−12
−2(x−12		4(x−12

podstawowy wykres przesunięty w lewo o ¹₂ i w dół o ¹₂ czerwony wykres jest tym którego szukasz