Wykaż, że promień okręgu opisanego na trójkącie Tachi: Proszę o pomoc z zadaniem: Wykaż, że promień okręgu opisanego na trójkącie równoramiennym o ramieniu długości a i podstawie długości b wyraża się wzorem: R= ^a2 _{√4a² − b}

Janek191: Napisz ułamek korzystając z litery U

Tachi:

a2
√4a2 − b

Adamm:

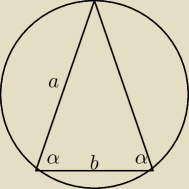
	a
z tw. Sinusów mamy R=
	2sinα

sinα=h/a

	1
h=√a2−		b2
	4

	a2
stąd R=
	√4a2−b2

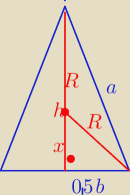
Janek191: Mamy

	a*b*c
P =
	4 R

P = 0,5 b*h h² = a² − 0,25 b² h = √a² − 0,25 b² zatem

	a2*b
0,5 b*h =		/ : b
	4 R

	a2
0,5 h =
	4 R

	a2
0,5 √ a2 − 0,25 b2 =
	4 R

a² = 4 R*0,5 √ a² − 0,25 b² a² = 2 R √a² − 0,25 b²

	a2		a2
R =		=
	2 √ a2 − 0,25 b2		√4 a2 − b2