Uzasadnij, że jest ponad 2000 liczb pięciocyfrowych podzielnych przez 5 Szczepan: Treść zadania: Uzasadnij, że jest ponad 2000 liczb pięciocyfrowych podzielnych przez 5, w których mogą występować cyfry: 0, 1, 2, 3, 4, 5. Wiem że takie zadanie widnieje już na forum, niestety zostało omówione w sposób którego nie rozumiem. Mam nadzieję że znajdzie się osoba chcąca mi pomóc. Bardzo dziękuję i miłego dnia życzę Szczepan

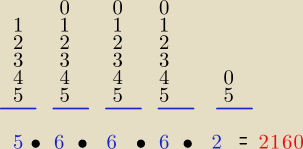
Adamm: pierwsza liczba 5 wybory, druga 6, trzecia, 6, czwarta 6, piąta 2 więc jest 4*5*5*5*2 takich liczb 5*6*6*6*2=2160

Adamm: 5 wyborów*

Adamm: 4, bo cyfra dziesiątek tysięcy ≠0, a 2 bo to warunek podzielności przez 5

Adamm: 5 nie cztery

Adamm: dobra namieszałem trochę, poprawnie jest 5*6³*2=2160

Eta:

Szczepan: Dziękuję za szybką i profesjonalna pomoc !

lolll: dalej nic nie rozumiem, dlaczego wybrać trzeba było 6 a nie np 4 ?

wredulus_pospolitus: Bo nie ma powiedziane że cyfry w tych liczbach NIE MOGĄ się powtarzać Związku z tym, jedynie mamy warunek do pierwszej cyfry (nie może być to 0) i do ostatniej (musi to być 0 lub 5), a reszta są dowolne (z dostępnych sześciu cyfr).