graficznie
Jack: rozwiaz nierownosc graficznie
|x| > |y+1|
5 wrz 15:33
Adamm: czym jest y? zmienną? funkcją? jeśli tak to jaką? chodzi ci o oś y?
5 wrz 15:45
jc: Narysuj zbiór |x| = |y+1|. Są to dwie proste y=−1+x, y=−1−x. Proste te dzielą płaszczyznę
na 4 części, te po bokach to rozwiązanie.
5 wrz 15:54
Mila:
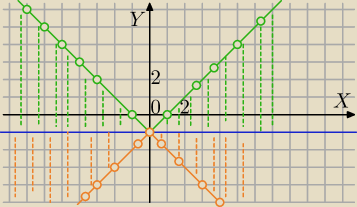
|y+1|<|x|
1)
|y+1|=y+1 dla y≥−1 (obszar nad prostą y=−1)
y+1<|x|
y<|x|−1 punkty nad prostą y=−1 i poniżej wykresu funkcji y=|x|−1
2)
|y+1|=−y−1 dla y<−1
−y−1<|x|
−y<|x|+1
y>−|x|−1
5 wrz 15:58
jc: Dzień dobry Mila

5 wrz 16:21
Jack: Dziekuje bardzo.
5 wrz 16:33
5 wrz 16:36
Mila:
Witam Panów

5 wrz 16:37
Jack: @Milu
Czy dobrze odczytuje polecenie, że jak jest Re to chodzi o część rzeczywistą , a jak Im to
urojoną do narysowania?
W takim razie w podpunkcie c) mam narysowac Re od (iz) ?
jak potraktowac Re?
mam, ze z2 = 2 Re(iz)
z = x+iy
x2 + 2xyi − y2 = 2 Re(ix−y)
i teraz...? hmmm
5 wrz 16:42
Adamm: Re(iz)=−Im(z)
5 wrz 16:51
Jack: @Adamm
niestety, ale to mi nic nie mowi.
5 wrz 16:54
Adamm: z=a+ib
iz=ia−b
5 wrz 16:57
Jack: no to akurat wiem

ale chodzi mi , co zrobic z tym Re?
5 wrz 16:57
Adamm: w twoim przypadku −Im(z)=−y
5 wrz 16:58
Adamm: Re to część rzeczywista
5 wrz 16:58
Jack: skoro Im(z) = y, a Re(iz) = − Im(z) to Re(iz) = − y
czyli za Re(iz) mam po prostu wstawic −y?
5 wrz 17:02
Adamm: tak
5 wrz 17:03
Jack: oki
5 wrz 17:03
Mila:
c) x2−y2=−2y
x2=y2−2y
5 wrz 17:13
Jack: tak, juz zrobilem, dzieki

5 wrz 17:16
 |y+1|<|x|
1)
|y+1|=y+1 dla y≥−1 (obszar nad prostą y=−1)
y+1<|x|
y<|x|−1 punkty nad prostą y=−1 i poniżej wykresu funkcji y=|x|−1
2)
|y+1|=−y−1 dla y<−1
−y−1<|x|
−y<|x|+1
y>−|x|−1
|y+1|<|x|
1)
|y+1|=y+1 dla y≥−1 (obszar nad prostą y=−1)
y+1<|x|
y<|x|−1 punkty nad prostą y=−1 i poniżej wykresu funkcji y=|x|−1
2)
|y+1|=−y−1 dla y<−1
−y−1<|x|
−y<|x|+1
y>−|x|−1


 ale chodzi mi , co zrobic z tym Re?
ale chodzi mi , co zrobic z tym Re?
