Funkcje Nwm: Wykaz ze funkcja określona wzorem f(x)=1/2x² − 1 jest malejąca w zbiorze (−nieskończoności, 0) przy 0 nawias ostry Wiem że Z: f(x)=1/2x² − 1, x1, x2 należy do przedziału powyżej i x1 >x2 T: f (x1)>f(x2) F(x1)− f(x2) .... = 1\2 x1² − 1/2 x2² I z tego wychodzi ze F(x1)− f(x2) <0 Czyli f jest rosnąca a powinna być malejąca. Co tu jest źle?

grthx:

	1
y=
	x1−1

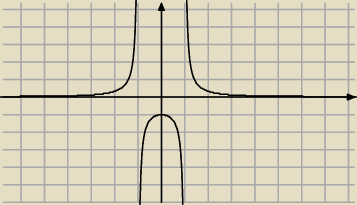
Pewnie zle okresliles przedzial

Janek191: Ma być w założeniu x₁ < x₂ bo x₁,x₂ < 0

Janek191:

	1
f(x) = 0,5 x2 − 1 czy f(x) =		− 1 ?
	2x2

Adamm: x₁,x₂∊(−∞;0>, x₁>x₂ funkcja jest malejąca jeśli f(x₁)<f(x₂) 1/2x₁²−1<1/2x₂²−1 x₁²<x₂² |x₁|<|x₂| x₁>x₂, udowodnione

Adamm:

	x2
zakładam że f(x)=		−1
	2

Nwm: Adam F (x) =0.5 x² − 1

grthx:

x2		1
	=
2		x2

Janek191: @ grthx: Co Ty wypisujesz ?

	1
x−2 =		!
	x2

grthx:

	1
Miałem napisac =		x2
	2

a napisałem