Wykresy funkcji grthx: dane sa dwie funkcje y=f(x) i y₁−=g(x) obie określone w tej samej dziedzinie D Podaj warunek konieczny i dostateczny nato aby 1. wykresy tych funkcji były symetryczne względem prostej y=k 2. Wykresy tych funkcji były symetryczne względem prostej x=p dziekuje

Adamm: y₁−=g(x)

Janek191: y₁ = g(x)

grthx: tak . Przez przypadek ten minus się zapisal

Adamm: 1. f(x)=−g(x)+h, h∊R to jest warunek konieczny i dostateczny dla istnienia takiej prostej y=k 2.f(x+h)=g(−x), to jest warunek konieczny i dostateczny dla istnienia takiej prostej x=p

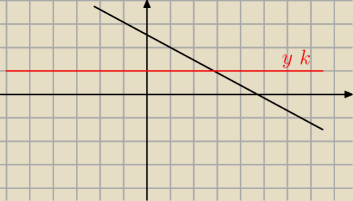
grthx: jeśli można to prosiłbym bardzo o wyjaśnienie na tym rysunku Narysowalem sobie jakiś tam wykres funkcji liniowej (dla przykładu i wykres y=2 Może latweij mi będzie na tym rysunku

Adamm: dla funkcji f(x)=mx+c, masz f(x)=−g(x)+h g(x)=−mx−c+h w punkcie przecięcia się prostych, czyli 2f(x)−h=0 rozwiązanie x₀ dla tego przypadku y=x₀ jest żądaną prostą, podobnie z 2.

grthx: Dobrze Adamm a możesz mi wytlumaczyc co oznacza u Ciebie h? To zadanie mam oznaczone jako trudne . Dlatego nie bardzo to rozumiem

Adamm: popatrz na symetrię z osią ox, f(x)=−g(x) jeśli teraz przesuniesz funkcję f(x) o wektor, to dla zachowania symetrii względem funkcji stałej to wektor musi być postaci v^→[0,h] gdzie h jest dowolne

Adamm: h to stała

grthx: Dziekuje CI bardzo .