trygonometria zbiór wartości funkcji
jadwiga: wyznacz zbiór wartości funkcji:
f(x)= sinx*ctgx−cosx*tgx ⇒ f(x)=cosx−sinx ⇒ ?
3 wrz 18:12
Janek191:
| | cos x | | sin x | |
f(x) = sin x* |
| − cos x* |
| = cos x − sin x |
| | sin x | | cos x | |
3 wrz 18:16
3 wrz 18:18
Janek191:
3 wrz 18:19
Janek191:
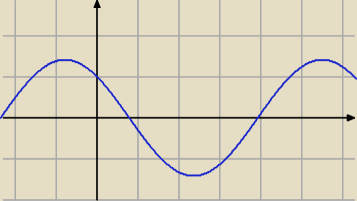
ZW = < − √2, √2 >
3 wrz 18:20
Janek191:
To jest wykres funkcji f

3 wrz 18:21
Adamm: a co z dziedziną?
3 wrz 18:21
Janek191:
| | π | |
− 1 ≤ cos ( |
| + x) ≤ 1 / * √2 |
| | 4 | |
−
√2 ≤ f(x) ≤
√2
ZW = < −
√2 , p{2] >
==================
3 wrz 18:22
Adamm: x≠πk ∧ x≠π/2+πk
3 wrz 18:24
Janek191:
Trzeba jeszcze wziąć poprawkę na dziedzinę :
3 wrz 18:26
jadwigaOrginals: proszę się nie podszywać pod jadwigę
3 wrz 18:26
Adamm: √2*cos(π/4)=√2*cos(−π/4)∉ZW
3 wrz 18:26
Janek191:
π − liczba "pi"
π ≈ 3,14
3 wrz 18:27
Adamm: tylko ten punkt ponieważ funkcja f(x) ma taki sam okres jak sin czy cos
3 wrz 18:28
jadwigaOrginals: janek wybacz za podszywającą się jadwigę piszącą durne komentarze
3 wrz 18:29
Janek191:
Korzystamy z wzoru
| | π | | π | |
cos x − sin x = √2*cos( |
| + x) = √2*sin ( |
| − x) |
| | 4 | | 4 | |
3 wrz 18:29
Mila:
Oryginalna Jadwigo, już jest w porządku?
3 wrz 18:36
jadwigaOrginals: jak najbardziej

3 wrz 18:38
Mila:
Pisz, jeśli się pojawi troll.
3 wrz 19:01


