Wartości parametru a Dominik: Dla jakich wartości parametru a równanie |5 – x| – | x+3| = a ma jedno rozwiązanie? Prosiłbym o jak najdokładniejsze opisanie tegoż zadanka.

Adamm: 1. 5−x≥0 ∧ x+3≥0 5≥x≥−3 5−x−(x+3)=a x=2−a 2. 5−x≥0 ∧ x+3<0 −3>x 5−x−(−(x+3)=a a=8 3. 5−x<0 ∧ x+3≥0 x>5 −(5−x)−(x+3)=−8=a Odp. równanie ma jedno rozwiązanie dla a≠−8 ∧ a≠8

Adamm: sorry, jeszcze dla pierwszego z założenia 5≥2−a≥−3 a≥−3 ∧ 5≥a a∊<−3;5>

Adamm: 5−x−(x+3)=a −2x+2=a x=1−a/2 5≥1−a/2≥−3 a/2≥−4 ∧ 4≥a/2 a≥−8 ∧ 8≥a ale a≠8 oraz a≠−8 więc a∊(−8;8)

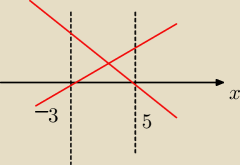
Macko z Bogdanca: Mozesz zrobisz tez tak jak Adamm ale z rysowaniem wykresu np |5–x|–|x+3|=a rysujesz zwykly wykres |5–x|–|x+3|. Dla kazdej liczby rzeczywsitej tak jak rozwiazujesz rownania x∊R⇔x∊(−∞,−3)u<3,5)u<5,∞) 1. x∊(−∞,−3) 2.x∊<−3,5) 3.x∊<5,∞) 5−x>0 ∧ x+3<0 5−x>0 ∧ x+3≥0 5−x≤0 ∧ x+3>0 (5−x)−(−x−3)=8 5−x−(x+3)=2−2x −5+x−x−3=−8

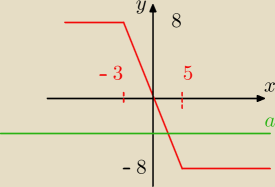
Macko z Bogdanca: i potem rysujesz i odczytujesz |5 – x| – | x+3| = a

Macko z Bogdanca: a∊(−8;8) poniewaz gdy a=−8 i a=8 to ma nieskonczenie wiele rozwiazan

Dominik: Dziękuje wam za pomoc