 sinx przyjmuje wartości dodatnie dla x∊<0,π> oraz wartości ujemne dla x∊(π,2π)
zatem
|sinx| = sinx dla x∊<0,π>
|sinx| = −sinx dla x∊(π,2π>
stąd wynika, że
|sinx|sinx = sinx*sinx = sin2x dla x∊<0,π>
|sinx|sinx = −sinx*sinx = −sin2x dla x∊(π,2π>
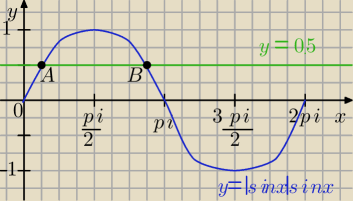
Nierówność |sinx|sinx ≤ 0,5, czyli (niebieski) wykres |sinx|sinx musi być pod (zielonym)
wykresem y=0,5.
Rozwiązaniem nierówności będzie zatem <0,xA> ∪ <xB,2π>
Musimy znaleźć współrzedne x−sowe punktów A i B
Rozwiązujemy w tym celu równanie |sinx|sinx = 0,5 w przedziale <0,π> bo w takim przedziale są
punkty A i B
Dla x∊<0,π> jest |sinx|sinx = sin2x więc do rozwiązania jest równanie
sin2x=0,5
sin2x − 0,5 = 0
sin2x − (√0,5)2 = 0
(sinx−√0,5)(sinx+√0,5) = 0
sinx − √0,5 = 0 lub sinx + √0,5 = 0
sinx = √0,5 lub sinx = −√0,5
sinx = √1/2 lub sinx = −√1/2
sinx przyjmuje wartości dodatnie dla x∊<0,π> oraz wartości ujemne dla x∊(π,2π)
zatem
|sinx| = sinx dla x∊<0,π>
|sinx| = −sinx dla x∊(π,2π>
stąd wynika, że
|sinx|sinx = sinx*sinx = sin2x dla x∊<0,π>
|sinx|sinx = −sinx*sinx = −sin2x dla x∊(π,2π>
Nierówność |sinx|sinx ≤ 0,5, czyli (niebieski) wykres |sinx|sinx musi być pod (zielonym)
wykresem y=0,5.
Rozwiązaniem nierówności będzie zatem <0,xA> ∪ <xB,2π>
Musimy znaleźć współrzedne x−sowe punktów A i B
Rozwiązujemy w tym celu równanie |sinx|sinx = 0,5 w przedziale <0,π> bo w takim przedziale są
punkty A i B
Dla x∊<0,π> jest |sinx|sinx = sin2x więc do rozwiązania jest równanie
sin2x=0,5
sin2x − 0,5 = 0
sin2x − (√0,5)2 = 0
(sinx−√0,5)(sinx+√0,5) = 0
sinx − √0,5 = 0 lub sinx + √0,5 = 0
sinx = √0,5 lub sinx = −√0,5
sinx = √1/2 lub sinx = −√1/2
| √2 | √2 | |||
sinx = | lub sinx = − | |||
| 2 | 2 |
| π | 3π | π | 5π | |||||
x = | + 2kπ lub x = | + 2kπ lub x = − | + 2kπ lub x= | +2kπ | ||||
| 4 | 4 | 4 | 4 |
| π | 3π | |||
Do przedziału <0,π> załapią się tylko xA= | oraz xB= | i to będą szukane | ||
| 4 | 4 |
| π | 3π | |||
Odp. Rozwiązaniem nierówności jest <0, | > ∪ < | ,2π> | ||
| 4 | 4 |
