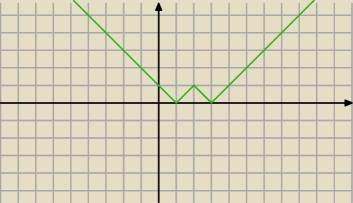
wartość bezwzględna Karolina: Mam narysować taką funkcje ktoś pomoże ? |2−|x−2|−1|

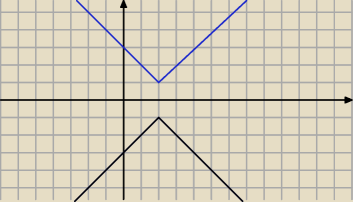
Oliwia9: f(x)= |−|x−2|−1| niebieski

===: dobre sobie

Adamm: |2−|x−2|−1|=|1−|x−2|| dla 1−|x−2|<0 ⇔ x−2<−1 ∧ x−2>1 mamy |x−2|−1 dla 1−|x−2|≥0 ⇔ −1≤x−2≤1 mamy 1−|x−2| stąd f(x)=1−|x−2| dla x∊<1;3> |x−2|−1 dla x∊(−∞;1)u(3;∞) 1−|x−2| dla x<2 to x−1 dla x≥2 to −x+3 |x−2|−1 dla x<2 to −x+1 dla x≥2 to x−3 porządkujesz f(x)=x−1 dla x∊<1;2) −x+3 dla x∊<2;3> −x+1 dla x∊(−∞;1) oraz x−3 dla (3;∞)

Karolina: O kurde, dzięki muszę to rozpracować.

Oliwia9: Taki jest podany wzor funkcji . Pewnie ma byc inny . ja nie bede w to ingerowac

===:

Adamm: poprawa f(x)=1−|x−2| dla x∊(−∞;1)u(3;∞) x∊<1;3> |x−2|−1 dla x∊<1;3> więc będzie f(x)=x−1 dla x∊(−∞;1) −x+3 dla x∊(3;∞) −x+1 dla x∊<1;2) x−3 dla x∊<2;3>

Jerzy: @Oliwia9 .. zastanów się....wszystke wartości ujemne z modułu ?

Adamm: nie, na początku było dobrze jednak

===: Oliwia9 ingerować nie musisz ale 2−1 to nie −1

Oliwia9: Bardzo przepraszam Taki babol z mojej strony dzieki za zwrocenie uwagi ===

===: ... tylko się nie gniewaj

Oliwia9: W zadnym wypadku

===:

jc: A jak będzie wyglądał wykres funkcji y = | | | x | − 2 | − 1| ?

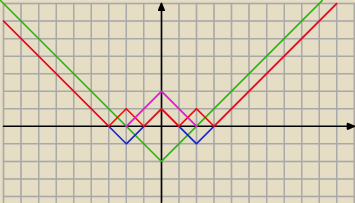
Jerzy: Ten czerwony

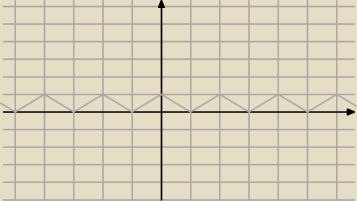
jc: Było 7 dzióbków. A ile dzióbków ma wykres y = | | | | x | − 4 | − 2| − 1| ?

Adamm:

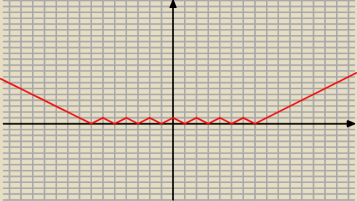
Adamm: w większej skali

Adamm: 15

jc: Dalej będzie pewnie 31, 63, 127, ...