dowody nierownosci
Krzysiek58: Udowodnij twierdzenia
| | a+b | |
a) dla kazdego ab∊R (a<b ⇒a< |
| <b |
| | 2 | |
Tutaj mamy koniunkcje nierownosci wiec rozbilbym tą (tę) nierownosc podwojna na dwie
nieronosci
czyli
i
| | a+b | |
(1) |
| <b to a+b<2b dla a<b ta nierownosc jest prawdziwa |
| | 2 | |
| | a+b | |
(2) |
| >a to a+b>2a dla a<b tez ta nierownosc jest prawdziwa |
| | 2 | |
Pytanie .
czy teraz nalezy tutaj skorzystac z tego ze mamy dwa wyrazenia prawdziwe wiec koniunkcja tych
wyrazen jest tez prawdziwa ?
30 sie 23:24
jc: Proponuję coś podobnego.
| | a | | c | | a | | a+c | | c | |
a,b,c,d >0. Jeśli |
| < |
| , to |
| < |
| < |
| |
| | b | | d | | b | | b+d | | d | |
30 sie 23:28
Krzysiek58: jc
Popracuje nad tym . To jest juz trudne w tej chwili
30 sie 23:34
Krzysiek58: ja naprawde postarm sie to przemyslec i dzisiaj albo jutro napisze odpowiedz .
30 sie 23:37
Janek191:
1)
a < b ⇒ a + a < a + b i a + b < b + b
2a < a + b i a + b < 2 b
więc
2a < a + b < 2b / : 2
==============
31 sie 08:16
Krzysiek58: mam tutaj zalozenie ze
| | a | | c | |
a, b c d jest dodatnie i |
| < |
| |
| | b | | d | |
| | a | | c | |
czyli tutaj nie moge zapisac ze |
| − |
| <0 bo to nie bedzie prawda |
| | b | | d | |
Jedynie co to chyba moge skorzystac z proporcji
| a | | c | |
| < |
| to ad<cb ale co dalej ? |
| b | | d | |
31 sie 08:19
Krzysiek58: Witaj

31 sie 08:20
Krzysiek58: nagorzej denerwuje mnie to z e jest to wlasnosc pochodnej proporcji i a ja tego nie potrafie
udowodnic
31 sie 08:41
Omikron: Z zał.
ad<cb / +ab
ad+ab<cb+ab
a(b+d)<b(a+c) / /b(b+d)
Drugą nierówność podobnie udowadniasz.
31 sie 08:59
Krzysiek58: Czesc

Tak po ludzku . dlaczego dodajesz tutaj do obu stron nierownosci +ab ?
Znalazlem podobne rozwiazanie (ale wlasnie tego nie rozumiem
mam proprcje
Od tego moge sobie utworzyc proporcje pochodne
| | b | | d | | b | | a | | d | | c | |
czyli |
| = |
| lub |
| = |
| lub |
| = |
| |
| | a | | c | | d | | c | | b | | a | |
Inne proprcje pochodne rowniez
To wiem ale jak przychodzi do udowodnienia tych nierownosci to nie bardzo wiem .
31 sie 09:56
Omikron: Dodaję, żeby wyszło co trzeba

Najpierw zrobiłem najprościej, czyli wyszedłem od tezy i zauważyłem, że ab się redukuje.
Później, żeby było perfekcyjnie od końca zapisałem.
31 sie 10:00
Krzysiek58: Korzstajac z Twojej rady zrobilem tak
(a+c)*d<(b+d)*c
ad+cd<bc+cd
ad<bc
Tak moze byc ?
31 sie 13:33
Omikron: Tak
31 sie 13:42
Krzysiek58: Dobrze ale Ty zapisales to od konca wiec bedzie tak
ad<bc
ad+cd<bc+cd
(a+c)*d<(b+d)*c
31 sie 13:42
Omikron: No tak, oba sposoby poprawne, ale wyjście z założenia najlepsze
31 sie 13:43
Krzysiek58: Dziekuje

31 sie 13:46
Omikron: 
31 sie 13:47
edgar:
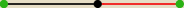
Mają tu panowie po prostu wzór na współrzędną x środka przedziału a; b . Środkowe wyrażenie
| | a+b | |
|
| sytuuje się w tej prostej interpretacji geometrycznej dokładnie w połowie odcinka |
| | 2 | |
a,b, na osi x
1 wrz 11:30


 Tak po ludzku . dlaczego dodajesz tutaj do obu stron nierownosci +ab ?
Znalazlem podobne rozwiazanie (ale wlasnie tego nie rozumiem
mam proprcje
Tak po ludzku . dlaczego dodajesz tutaj do obu stron nierownosci +ab ?
Znalazlem podobne rozwiazanie (ale wlasnie tego nie rozumiem
mam proprcje
 Najpierw zrobiłem najprościej, czyli wyszedłem od tezy i zauważyłem, że ab się redukuje.
Później, żeby było perfekcyjnie od końca zapisałem.
Najpierw zrobiłem najprościej, czyli wyszedłem od tezy i zauważyłem, że ab się redukuje.
Później, żeby było perfekcyjnie od końca zapisałem.


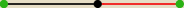 Mają tu panowie po prostu wzór na współrzędną x środka przedziału a; b . Środkowe wyrażenie
Mają tu panowie po prostu wzór na współrzędną x środka przedziału a; b . Środkowe wyrażenie