Wykres funkcji, wyznaczanie wartości parametru m Qwadrat: Wykonaj wykres funkcji

	2x−3
f(x)= |		|
	x+1

Wyznacz te wartości parametru m, dla których równanie f(x)=m ma dwa rozwiązania przeciwnych znaków.

Jerzy:

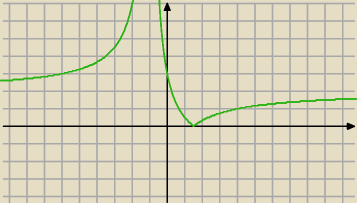
	2(x+1) − 5		5
f(x) =		= −		+ 2
	x+1		x+1

przesuwaj linikę wzdłuż osi OY i patrz kiedy spełnia warunek

Qwadrat: Wykażę się teraz sporą niewiedzą/głupotą, ale w końcu chodzi o to żebym się nauczył, zatem: To 'przekształcenie' f(x), które wykonałeś jest konieczne? Nigdy bym nie wpadł na takie coś. Masz jakiś sposób na rysowanie takich wykresów? Przy mojej pierwszej próbie najpierw zrobiłem sobie tabelkę z 'x' i 'f(x)' (gdzie za 'f(x)' przyjąłem wzór podany w poleceniu) i wypisałem w niej wartości dla x={−3,−2,0,1,2,3} w konsekwencji czego pominąłem to odbicie na x=1.5. Skąd powinienem wiedzieć, żeby sprawdzić akurat x=1.5? I koniec końców, te dwa rozwiązania przeciwnych znaków: Rozumiem że chodzi o to, żeby w linii poziomej były 2 rozwiązania, z czego jedno ma być po lewej strony osi OY, a drugie ma być po prawej stronie tej osi, więc pod uwagę biorę tylko przedział <0,3>, przy czym: − na y=0 jest tylko jeden punkt, − na y=2 wydaje mi się że jest asymptota pozioma i po lewej stronie osi funkcja nie osiąga tej wartości, − na y=3 nie ma punktu po prawej stronie, − dla y∊(0,2) są po 2 punkty po prawej i nie ma rozwiązań po lewej, Więc z tego wynika mi, że równanie f(x)=m ma dwa rozwiązania przeciwnych znaków dla m∊(2,3). Jeśli coś w moim myśleniu jest błędne to prosiłbym o nawrócenie mnie na właściwą drogę, wszelkie wskazówki również mile widziane. I dzięki już nawet za sam czas poświęcony na czytanie tego.

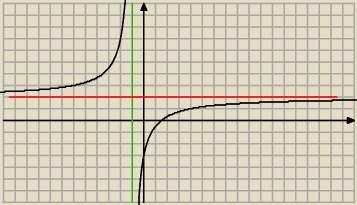
Krzysiek58: To przeksztalcenie jest potrzebne . Doprowadzasz w ten sposob wyrazenie ktore jest wewnatrz wartosci bezwzglednej do postaci kanonicznej tak samo ja funkcje wymierna (homograficzna .

	−5
Teraz rysujemy sobie ta hiperbole y=		+2
	x+1

WIdzisz ze asymptota pionowa to x=−1 i pozioma to y=2 Ale my mamy ten wzor w wartosci bezwzglednej wiec musmy te zcesc wykresu co jest pod osia OX dac nad os OX (bo wartosc bezwzgledna jest zawszse nieujemna czyli rowna 0 badz wieksza od zera . Na rysunku Jerzego masz ta sytuacje juz po odbiciu .

Krzysiek58: Co do rozwiazan to myslenie prawidlowe

piotr1973: m∊(2;3>

Jerzy: m ∊ (2,3)