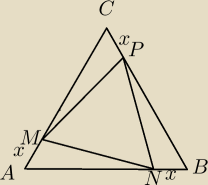
Trojkat rownoboczny ABC Macko z Bogdanca: Trojkat rownoboczny ABC ma bok dlugosci 20 cm. Na jego bokach obrano pkt M,N,P tak,że AM=BN=CP. Oznacz dlugosc odcinkow AM,BN oraz CP litera x Napisz wzor funkcji pola trojakta MNPw zaleznosci od dlugosci x. Jak nalezy wybrac punkty M,N,P alby pole trojakta MNP bylo najmniejsze? Robie to tak. Czy jest to dobrze wykonane? L_ABC=60cm AB=BC=AC=20cm PB=AN=MC=20−x ΔABC i ΔMNP sa rownoboczne wiec ich katy maja miare 60 stopni ΔAMN~ΔMCP~ΔNBP oraz ΔABC~ΔMNP

	a2√3
Pole trojkata rownobocznego P=
	4

Korzystam z twierdzenia cosinusow

	1
PN2=(20−x)2+x2−2[x(20−x)]		x∊(0,20)
	2

	1
PN2=400−40x+2x2−(40x−2x2)
	2

PN²=400−40x+2x²−20x+x² Pn²=400−60x+3x² podstawiam PN² pod a² we wzorze na pole trojkata

	PN2√3		(400−60x+3x2)√3
P(x)=		=
	4		4

	3
P(x)=(100−15x+		x2)√3
	4

	3√3
P(x)=		x2−15√3x+100√3
	4

	15√3		60√3
b) xw=		=		=10
	6√3   4		6√3

bok trojakta ABC wynosi 20cm wiec 20:10=2 M,N,P powinny znajdowac sie w srodku boku trojata ABC aby pole tego trojata (MNP) bylo najmniejsze.

Jack: nie czytalem calego ale wzor na pole powinien sie zgadzac, a pole bedzie najmniejsze gdy to beda srodki bokow wiec to tez sie zgadza, wiec calosc pewnie dobrze, ale moze ktos jeszcze wyrazic opinie ; D

Macko z Bogdanca: Ok dzieki

piotr: P=20²√3/4−3x/2(20−x)√3/2

Jurand: Bez twierdzenia cosinusów: a − długość boku trójkąta ABC

	√3
Pole trójkąta MNP: PMNP = P(x), sin60 =
	2

	1		1		√3
P(x) = PABC − 3*PANM, P(x) =		a2√3 − 3*		*x*(a − x)*
	4		2		2

	√3
P(x) =		(3x2 − 3ax + a2),
	4

y = 3x² − 3ax + a² jest parabolą, która posiada najmniejsza wartość

	3a		a
dla x =		=
	6		2