monotonicznos hiperboli 6.167 : Witam mam problem poniewaz nie bardzo rozumiem przedzialu monotonicznosci hiperboli a mianowicie np 1u{x} no i moje pytanie brzmi dlaczego ona rosnie w przedziale od (−inf,0)u(0,inf) skoro hiperbola nie dotyka zera dziekuje za pomoc

6.167 : ¹_x

2.016: to jakieś bazgroły, napisz wyraźniej

6latek :

	1
y=		jest funkcja malejaca a nie rosnaca
	x

2.016:

	1
Wykres y =		tak wygląda, nigdzie nie rośnie
	x

6.167 : jasne a wiec dlaczego funkcja ¹_x jest malejaca w przedzialach (−nieskonczonosc ,0)u (0 +nieskonczonosc)

6latek : Juz wtym samym zapisie twoim jest przeciez ze 0 nie nalezy do tych przedzialow Ale ja nie jestem pewiem czy za taki zapis nie bedziesz mial odjete punkty to znaczy suma przedzialow

6latek :

	1
poza tym y=		gdzie x≠0 bo wiadomo ze przez 0 dzielic nie wolno
	x

6.167 : tak tak to wiem natomast kompletnie nie rozumiem tej hiperboli wiem jak ja narysowac ale nie mam pojecia co z tymi przedzialmi dlaczego maleje a nie rosnie itp

Benny: Funkcja nie jest monotoniczna w sumie przedziałów.

6latek :

	2
To jest wykres y=−
	x

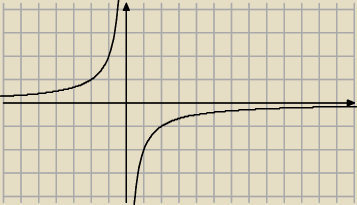
jaka to bedzie funkcja rosnaca przedzialami czy malejaca ? (patrz na wykres

Omikron: Pomiędzy przedziałami przy ustalaniu monotoniczności nie powinno być znaku sumy, tylko przecinek. Maleje...bo cały czas idzie w dół. Jest malejąca jeżeli zawsze dla x₁<x₂ f(x₁)>f(x₂) I dlatego ważny jest ten przecinek, bo sprawdź sobie np. dla x₁= −3 i dla x₂=1

6latek : Post Omikrona byl do sytuacji z 22:58 Ty mozesz sobie zapamietac tak Jesli wykres hiperboli lezy w 1 i 3 cwiartce to funkcja jest malejaca przedzialami Jesli wykres hiperboli lezy w 2 i 4 cwiartce to funkcja ta jest rosnaca przedzialami .

6.167 : ooo super dziekuje

6.167 : naprawde jestem bardzo wdzieczny a mam pytanie odnosnie przedzialow np ⁻³_x to jaki ona ma przedzial zeby f przyjmowala wartosci wieksze od −3

Omikron: Narysuj wykres i odczytaj rozwiązanie. Alternatywnie rozwiąż nierówność f(x)>−3 ale to tylko jeżeli na rozszerzeniu jesteś.

daras: jest malejąca, ponieważ dla każdego x₁<x₂ : f(x₁) > f(x₂)