Przekształcenia funkcji auoy: Mam takie zadanie: Opisz sposób, w jaki należy przekształcić wykres funkcji f aby otrzymać wykres funkcji g, gdy: a) f(x) = sin3x ∧ g(x) = sin(3x+π) b) f(x) = 2x² ∧ g(x) = 2x²−12x+12 byłabym wdzięczna za pomoc

Rafał: a) g(x)=sin(3x+π)=sin( 3(x+π/3) )=f(x+π/3) wystarczy przesunąć wykres funkcji f o π/3 w lewo.

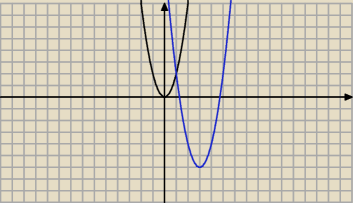
zef: B można narysować i przyjrzeć się obu wykresom, wystarczy tylko kilka punktów tj: wierzchołek i jakiś punkt który leży na ramieniu paraboli. Widać że wykres został przesunięty o 3 w prawo i 6 w dół

Mila: g(x) = 2x²−12x+12

	−b		12
p=		=		=3
	2a		4

g(3)=q=−6 g(x)=2*(x−3)²−6 Wykres powstał po przesunięciu wykresu f(x) o wektor [3,−6] , tak jak napisał zef

auoy: dziękuję