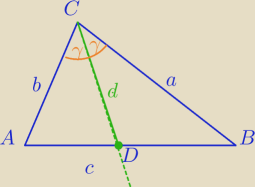
trójkat klaudyna: Niech ABC będzie trójkątem o bokach a,b, c.Niech dwusieczn kata C przecina AB w D. Wykaż że długość CD wynosi:

	C   2ab cos   2
	a+b

Jack: z tymi zadaniami mam zawsze taki klopot ze jest za duzo mozliwosci by to udowodnic i czesto wychodzi cos innego np. teraz wyszlo mi

	bc cos 2α
|CD| =
	(b+c) cos α

co jest bliskie prawdy ale jednak nadal dalekie od tego co chca...

klaudyna: no ale to musi być ten wzór podany

Mila:

	1		1
PΔABC=		*a*b*sin(2γ)=		*a*b*2*sinγ*cosγ
	2		2

	1		1
PΔABC=		*b*d*sinγ+		*a*d*sinγ ⇔
	2		2

1		1		1
	*a*b*2*sinγ*cosγ=		*b*d*sinγ+		*a*d*sinγ ⇔
2		2		2

2a*b*cosγ=b*d+a*d⇔ 2a*b*cosγ=d*(a+b)

	2a*b*cosγ
d=
	a+b

==========