Graf
xDDD:
Uzasadnij, że każdy graf jednorodny stopnia 2 jest rozłączną sumą cykli.
24 sie 11:03
jc: Indukcja względem liczby wierzchołków.
Wychodzisz z jakiegoś wierzchołka i po pewnej liczbie kroków wracasz
do niego (na pewien wierzchołek musisz trafić po raz drugi i pierwszym takim
wierzchołkiem będzie wierzchołek, z którego wyszedłeś). Pozostała część grafu
z założenia indukcyjnego będzie sumą rozłącznych cykli.
24 sie 11:15
xDDD: Mógłbym prosić o chłopskie wytłumaczenie?
24 sie 12:41
Xddd: Ktoś tu jeszcze siedzi?
24 sie 22:27
jc: Stopień każdego wierzchołka = 2, tzn. z każdego wierzchołka wychodzą dwie kreski.
Wyruszasz z jakiegoś wierzchołka. Zaznaczasz przebyte krawędzie. Jak już wybierzesz
kierunek, to droga sama Cię poprowadzi (dlaczego?). Wędrówkę musisz skończyć
(masz skończoną liczbę wierzchołków). Skończysz na wierzchołku z którego wyszedłeś
(gdybyś natrafił na wierzchołek, w którym już byłeś, wierzchołek ten, w brew założeniu
miałby stopień co najmniej 3). A zatem zamknąłeś pewien cykl.
Pozostały graf traktujesz tak samo.
Czego nie rozumiesz?
24 sie 23:14
pomoooocy: Dzięki za odpowiedź mój najlepszy kolego JC. Chciałbym zrozumieć co to znaczy:
−graf jednorodny
−co to znaczy, że stopnia 2 (jak sie domyślam, że z każdego wierzchołeka idą 2 krawędzie)
− co to rozłączna suma cykli
Z góry dzieki, jesteś dobrym matematykiem. Po studiach matematycznych?
Czy geniusz samouk?
24 sie 23:31
jc: Nie wiem, co to znaczy graf jednorodny. Podejrzewam, że w zadaniu chodzi o taki graf,
w którym z każdego wierzchołka wychodzą dwie krawędzie.
Cykl to ciąg wierzchołków np. a,b,c,d,e połączonych krawędziami
a − b, b − c, c − d, d − e, e −a.
Rozłączne cykle to cykle (czyli takie zamknięte drogi), które nie mają wspólnych
wierzchołków.
24 sie 23:56
xDDD: Tutaj wyjaśnienie co to graf jednorodny:
Jeśli stopnie wszystkich wierzchołków grafu G są równe δ
to graf G nazywamy grafem jednorodnym stopnia δ
28 sie 17:36
xDDD:
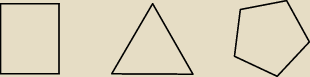
W skrócie chodzi o to, że od każdego punktu w grafie idą 2 krawędzie?
Czyli graf jednorodny stopnia 2 wyglądać może tak?
28 sie 18:16
jc: Właśnie tak musi wyglądać nasz graf

28 sie 18:38
xDDD: A mógłbyś pokazać jak wygląda rozłączna suma cykli a jak nierozłączna

28 sie 19:22
xDDD: Prosze o pomoc
28 sie 23:23
jc: Rozłączna suma wygląda tak, jak na Twoim rysunku (3 rozłączne cykle).
28 sie 23:35
xDDD:
No to skoro mam taki graf to gdzie tu jest rozłączna suma cykli?
29 sie 00:34
29 sie 09:25
Krzysiek58: Ale wlasnie CI pomagam . Podalem literature gdzie mozesz o tym przeczytac
Mozesz sobie przeciez wypozycz ksiazke
29 sie 10:33
xDDD: W takim razie po co dodajesz własne zadania? Skoro możesz
wypożyczyć sobie książke i o tym przeczytać.
29 sie 10:54
Krzysiek58: xDDD
jesli zauwazyles to tez pytam o literature
Poza tym jest duza roznica miedzy nami . Ja juz nie musze bo dawno juz sie nie ucze(ale chce .
natomiast Ty musisz bo jestes studentem

Ja naprawde nie chce Ci dokuczyc bo po co . Wpisalem na allegro teoria grafow i wyskoczylo
miedzy innymi to
29 sie 11:07
xDDD: Jest ktoś chętny do pomocy?
30 sie 21:49
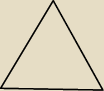
xDDD: 
1 wrz 13:31
jc: Ten trójkąt jest to też suma, ale składająca się z jednego cyklu

Gdyby nie było żadnego składnika, też moglibyśmy powiedzieć, że mamy sumę
(to sprawa umowna).
1 wrz 15:15
 W skrócie chodzi o to, że od każdego punktu w grafie idą 2 krawędzie?
Czyli graf jednorodny stopnia 2 wyglądać może tak?
W skrócie chodzi o to, że od każdego punktu w grafie idą 2 krawędzie?
Czyli graf jednorodny stopnia 2 wyglądać może tak?


 No to skoro mam taki graf to gdzie tu jest rozłączna suma cykli?
No to skoro mam taki graf to gdzie tu jest rozłączna suma cykli?
 Ja naprawde nie chce Ci dokuczyc bo po co . Wpisalem na allegro teoria grafow i wyskoczylo
miedzy innymi to
Ja naprawde nie chce Ci dokuczyc bo po co . Wpisalem na allegro teoria grafow i wyskoczylo
miedzy innymi to

 Gdyby nie było żadnego składnika, też moglibyśmy powiedzieć, że mamy sumę
(to sprawa umowna).
Gdyby nie było żadnego składnika, też moglibyśmy powiedzieć, że mamy sumę
(to sprawa umowna).