 ZAD 1.
Oblicz pole truJkata ograniczonego porostymi y= 2x−2 i y=−x+4 oraz osia x
ZAD 2.
Okrag o środku C ma promień o długości 5 cm, a okrąg o środku B ma promień długości 3 cm.
Podaj
długość odcinka BC, jeśli okręgi sa styczne wewnętrznie.
ZAD 3.
Trójkat prostokątyny ma przyprostokątne długości 9cm i 12cm. Na trójkacie opisano i na
trójkacie wpisano okrąg. Oblicz sume długości średnicy tych okręgów.
ZAD 1.
Oblicz pole truJkata ograniczonego porostymi y= 2x−2 i y=−x+4 oraz osia x
ZAD 2.
Okrag o środku C ma promień o długości 5 cm, a okrąg o środku B ma promień długości 3 cm.
Podaj
długość odcinka BC, jeśli okręgi sa styczne wewnętrznie.
ZAD 3.
Trójkat prostokątyny ma przyprostokątne długości 9cm i 12cm. Na trójkacie opisano i na
trójkacie wpisano okrąg. Oblicz sume długości średnicy tych okręgów.
| AB * h | ||
podstawa: długość | ||
| 2 |
| AB * CD | ||
P = | = 3
| |
| 2 |
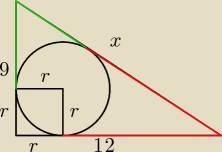 92 + 122 = x2
81 + 144 = x2
225 = x2
x=15
12−r + 9−r = x
21 − 2r = 15
−2r = −6
r=3
d=2r=6
średnica okręgu wpisanego to przeciwprostokątna
więc d+ d1 = 6+15 = 21
92 + 122 = x2
81 + 144 = x2
225 = x2
x=15
12−r + 9−r = x
21 − 2r = 15
−2r = −6
r=3
d=2r=6
średnica okręgu wpisanego to przeciwprostokątna
więc d+ d1 = 6+15 = 21