23 sie 19:41
Jack:
1) Po co chcesz to rozkladac
2) Mozesz tak
(x−3)2 * (x−3)2 = (x2−6x+9) * (x2−6x+9) = ...
23 sie 19:43
Yobo: A no właśnie nie wiedziałem że tak mogę. dzięki!
23 sie 19:45
Jack: mimo wszystko ja bym tego nie rozkladal...zadnego z nich.
23 sie 19:48
Yobo: Czyli jak mam rozwiązać te zadania?
23 sie 19:48
Jack:
jak bys mial h(x) = f(x) * g(x)
f(x) = (x−3)(x−1)2
g(x) = (x−2)2 * (x−5)
no to h(x) = (x−3)(x−1)2 * (x−2)2 * (x−5)
i jedynie szukasz tego czego chca w poleceniu a mianowicie chca
h(x) > 0
zatem
(x−3)(x−1)2 * (x−2)2 * (x−5) > 0
rysujemy tzw. wezyk i odczytujemy.
koniec.
Gdybys mial dodac albo odjac te funkcje −> ze by bylo h(x) = f(x) + g(x) to wtedy bys musial
rozlozyc.
23 sie 19:51
6latek : skorzystaj z ewzoru an*am= an+m
np (x−2)2*(x−2)3= (x−2)5
23 sie 19:51
Eta:
(x−3)4>0 ⇔ x∊R\ {3}
(x−3)4≥0 ⇔ x∊R
(x−3)2016 ≥0 ⇔ x∊R
wniosek dla wykładników parzystych.......
23 sie 19:55
Yobo: W 2.46 mam
−3(x−3)
2 i (x−2)
3
To po prostu z tego mam (x−5)
5 
23 sie 19:56
Jack: nie
jak masz takie same nawiasy tylko inne potegi
(x−2)2 * (x−2)3 = (x−2)5
to jest ze wzoru potegowego am * an = am+n ktory napisal juz 6latek
23 sie 19:58
Yobo: A to się tyczyło tego.
A jak najprościej tutaj dowiedzieć się czy rysuje od góry czy od dołu.
23 sie 20:01
Adam: jeśli chodzi o rysowanie wielomianu to rysujesz od prawej z góry dla współczynnika dodatniego,
jak chcesz z lewej musisz wziąć pod uwagę stopień wielomianu
23 sie 20:04
Jack:
jak masz minus gdzies przed nawiasami to od dolu, jak nie to od gory, oczywiscie od prawej
strony zaczynamy rysowac
np. jak masz
−3(x−2)(x−3)2(x−5)
to od dolu rysujesz
albo jak masz
(2−x)(x−3)(x+5)
tutaj tez od dolu bo masz 2−x wiec jak bys wymnozyl te wszystkie nawiasy to bys przy najwyzszej
potedze mial minus
a chodzi wlasnie o ta najwieksza potege przy iksie
natomiast tutaj bys dal plus czyli od gory
(x−3)(x+1)(x+3)(x−1)2
natomiast potegi przy tych nawiasach mowia czy wykres sie odbija czy przechodzi.
przy parzystych potegach np. (x−2)2, (x−1)4, x2, wykes sie odbija, natomiast przy x, (x−1),
(x−3)3 tutaj wykres sie nie odbija.
23 sie 20:04
Adam:
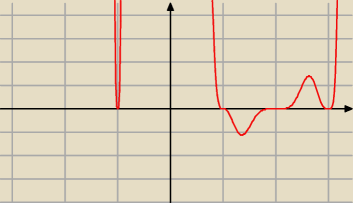
h(x)=(x−2)
5(x+1)
4(x−3)
4(x−1)
3
oczywiście twój rysunek ma być czysto poglądowy,
mamy x∊(−
∞;−1)u(−1;1)u(2;3)u(3;
∞)
23 sie 20:11
Yobo: Zapomniałeś o zerze
.
23 sie 20:15
Adam:
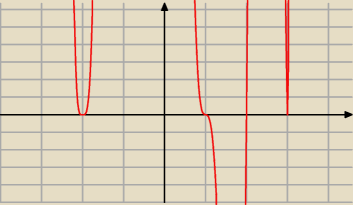
w 2 mamy h(x)=−(x−1)
3(x−3)
2(x+2)
4(x−2)
mamy wyznaczyć x dla których
−(x−1)
3(x−3)
2(x+2)
4(x−2)<0
(x−1)
3(x−3)
2(x+2)
4(x−2)>0
więc mamy x∊(−
∞;−2)u(−2;1)u(2;3)u(3;
∞)
23 sie 20:18
Yobo:
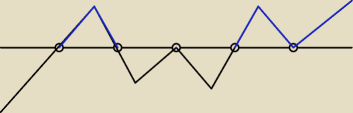
Mi wyszło że od góry.
Chociaż tu wychodzi że
(−1;0)∪(2;3)∪(3;
∞)
Ale w odp jest.
(−1;0)∪(2;3)∪(3;
∞)
(0;1)∪(2;3)∪(3;
∞)
23 sie 20:19
Yobo: W sensie ta ostatnia linijka jest w odpowiedziach a mi źle wychodzi.
23 sie 20:22
Adam:
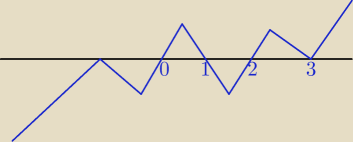
źle masz rysunek
23 sie 20:23
Adam: dla 1 mamy 3 potęgę więc funkcja przechodzi
23 sie 20:25
Adam: a dla −1 funkcja się odbija bo masz potęge 4
23 sie 20:25
Yobo: A no tak.
−14
a ja dałem 14
23 sie 20:26
