Zbadaj parzystość funkcji f
vivi: Zbadaj parzystość funkcji f:
b) f(x) =
√x
Proszę o pomoc
23 sie 13:39
Janek191:
d) Funkcja parzysta,bo
f(−x) = f(x)
23 sie 14:05
Janek191:
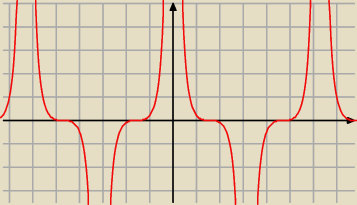
d)
23 sie 14:16
Adam: | | 3x+1 | | 3−x+1 | |
a) x≠0, f(x)=x2 |
| =(−x)2 |
| ≠f(−x) |
| | 3x−1 | | −3−x+1 | |
b) x≥0, oprócz dla x=0 nie istnieje −x, funkcja nie jest parzysta
| | 3−x | |
c) |
| ≥0, (x−3)(x+3)≤0, x∊<−3;3> |
| | 3+x | |
| | 3−x | | 3+x | | 3−(−x) | |
f(x)=xlog |
| =xlog( |
| )−1=(−x)log( |
| )=f(−x) |
| | 3+x | | 3−x | | 3+(−x) | |
d) x≠π/2+πk, k∊C
| | cosx | | cos(−x) | | cos(−x) | | cos(−x) | |
f(x)= |
| = |
| = |
| = |
| =f(−x) |
| | tg2x | | (−tgx)2 | | (tg(−x))2 | | tg2(−x) | |
23 sie 15:08
vivi: dziękuję
mam jeszcze jeden przykład: f(x) = |x|+x
23 sie 18:08
Adam: f(x)=|x|+x=|−x|+x≠f(−x)
23 sie 18:09
vivi: jeszcze raz dzięki
23 sie 18:11
vivi: a w pierwszym przykładzie jak ci wyszło, że w mianowniku 3−x−1 to −3−x+1 ?
23 sie 18:16
Adam: podzieliłem mianownik i licznik przez 3x
23 sie 18:17