Nierówności wielomianowe.
Yobo: (x2−4)(x2+x)(3−x)>0
x0=−2,2,3
(x2+x) A co z tym wielomianem?
23 sie 09:03
Jerzy:
x2 + x = x(x + 1)
23 sie 09:04
===:
x(x+1) .... czyli
23 sie 09:04
Yobo: 0 i −1 oki. dzięki.
23 sie 09:19
Yobo: 2x2(−−−)(−−−)
0 też może być pierwiastkiem który się odbija?
23 sie 09:40
Jerzy:
Może.
23 sie 09:42
Jack: tez moze byc.
23 sie 09:42
Yobo:
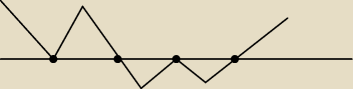
c)
2x
2(4x
2−1)(x
2+2x+1)≥0
2x
2(2x−1)(2x+1)(x+1)
2≥0
Jakby było >0
To
| | 1 | | 1 | |
(−∞,− |
| )∪( |
| , ∞) |
| | 2 | | 2 | |
23 sie 09:52
Jack: jakby bylo > 0
to
| | 1 | | 1 | |
x ∊ (− ∞ ; − 1) U (−1 ; − |
| ) U ( |
| ; ∞) |
| | 2 | | 2 | |
23 sie 09:57
Yobo: Czemu wgl 0 się dolicza do tego?
23 sie 10:31
Jerzy:
bo coś co ma być dodatnie, nie może równać się zero
23 sie 10:33
Yobo:
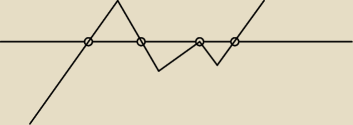
A jeśli mam < 0
dla przykładu
−3x
2(2+x)
3(x
2−3x−4)<0
x
0= −1,−2,0
2,4
xe(−2,−1)∪(4;
∞)
23 sie 10:44
6latek : Wykrwezyk nalezy dac od dolu
x3*x2= x5
x5*(−3x2)= −3x7 (wspolczynnik przy x7 jest ujemny wezyk od dolu
23 sie 11:06
23 sie 11:08
Yobo:
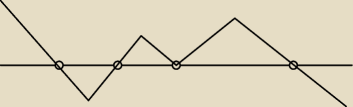
No to rozkładam czynniki
−3x
2(2+x)
3(x
2−3x−4)<0
√5Δ=5
x
1=−1
x
2=4
−3x
2(2+x)
3(x−4)(x+1)
x
0= −1,−2,0
2,4
−3x
5 (No bo jak rozłożę (x
2−3x−4) to już nie ma x
2.)
Wężyk od dołu.
xε (−2;−1)∪(4;
∞)
23 sie 11:20
6latek : NO bo jak rozloze x2−3x−4 to juz nie ma x2 .
A kto powiedzial ze nie ma x2 ?
przeciez x2−3x−4=(x−4)(x−1) \przecie z (x−4)(x+1) jest to postac iloczynowa wiec x*x=x2
Po rozlozeniu na czynniki mnozysz wszystkie xsy i patrzysz jaki jest znak
Dobrze byloby gdybys pisal cyfry (wtedy lepiej widac
23 sie 11:28
6latek : Teraz jest dobrze
23 sie 11:29
Yobo:
Ale jak jest <0 to patrzę tylko na
23 sie 11:35
6latek : Tak jak piszsesz patrzysz gdzie wezyk lezy pod osia
Dla >0 patrzysz gdzie wezyk lezy nad osia
23 sie 11:37