permutacja
permutacja: Ile jest permutacji f zbioru {1,2,3,4,5,6}, gdzie f(3)=1?
O co dokładnie chodzi z f(3)=1?
19 sie 17:48
Janek191:
Może tych permutacji jest 5 ! = 120 ?
19 sie 18:04
Benny: Permutacja jest to odwzorowanie bijektywne.
19 sie 18:16
Janek191:
Czy taka jest treść zadania − 17.48 ?
19 sie 18:17
Benny: Treść zadania jest dobra.
Wiemy, że f(3)=1
Jedną permutacją może być zatem
f(1)=2 f(2)=3 f(3)=1 f(4)=4 f(5)=5 f(6)=6
Dla trójki zawsze będzie wartość jeden, więc tak jak mówisz będzie 120 permutacji.
19 sie 18:20
permutacja: Dobra, czyli:
Na 1 miejscu będzie 5 liczb, na drugim 4 liczby, na trzecim tylko 1, bo takie jest założenie,
na czwartym 3, na piątym 2, a na ostatnim 1, ta?
19 sie 18:34
Saizou :
Można też tak:
wszystkich możliwych permutacji 6−elemetowego zbioru jest 6!,
przy czym f(3)=1, więc ta permutacja może występować na 6 miejscach...
19 sie 20:10
Mila:
Witaj Saizou, miałeś już na studiach funkcje tworzące?
19 sie 21:38
Saizou :
Cześć Milu, niestety nie.
19 sie 21:50
Saizou :
ale w tym semestrze będe mieć
19 sie 21:51
Mila:
To czekam, aż będziesz miał.
19 sie 21:51
Mila:
To poczytaj trochę, to jest ciekawe. Nie miałam tego na studiach.
Właśnie obliczyłam sumę
13+23+33+....+n3
za pomocą funkcji tworzącej.
Teraz pomęczę się z ciągami rekurencyjnymi.
Jeden łatwy już zrobiłam.
Może razem coś podziałamy.
Na forum nie ma co teraz robić, Maciusiowi wszyscy pomagają, nie chcę robić tłoku.
19 sie 21:56
Jack: ja zapewne niedlugo zaczne ostre przygotowania to bede miec mnostwo pytan : D
chociazby oto jak narysowac w ukladzie wspolrzednych w 3 wymiarach, bo nie mam pojecia jak
zaznaczyc
np punkt (1,1,1)
albo (−1,2,−4)
przeciez tego nie widac : D
19 sie 22:27
Mila:
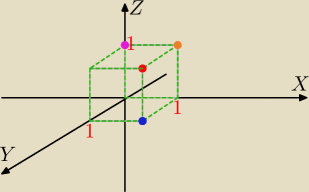
Widać, widać.
(1,1,1)
(0,0,1)
(1,1,0)
(1,0,1)
19 sie 22:42
Saizou :
ale tę sumę można obliczyć bez funkcji tworzących xd
19 sie 22:42
Saizou :
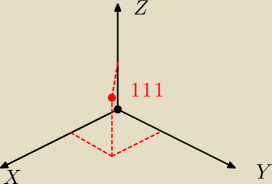
albo też tak
19 sie 22:45
Jack: Milu
Jak ida te wspolrzedne
myslalem ze to jest x y z
Czyli punkt (0,0,1) to ma na osi X zero, na osi igrek zero i na osi zet ma 1
Przy czym zawsze myslalem ze Z jwst ten 3 wymiar a iks i igrek jest jak w dwu wymiarze.
Szczerze mowiac wiecej widze na rysubku Saizou :{
19 sie 22:50
Mila:
Wiem, że można i to różnymi sposobami, ale chciałam zastosować funkcje tworzące.
19 sie 22:51
Saizou :
Jack wszystko zależy czy będzie rozpatrywać układy lewo− czy też prawoskrętne
19 sie 22:54
Mila:
Jack, każdy szuka własnej ścieżki do wiedzy, to co widzisz lepiej, to jest dobre dla
Ciebie.
19 sie 22:55
Saizou : Ile z tym zachodu
19 sie 23:04
Jack:
19 sie 23:05
Saizou : wyszło mi
| | n4 | | n3 | | n2 | |
∑k=1∞ k3 = |
| + |
| + |
| |
| | 4 | | 2 | | 4 | |
19 sie 23:33
6latek : Milu maciusiowi zostal tylko Omikron
To jak odnosi sie do wszystkich to jedna sprawa
Druga jest taka ze jak pomagajacy sie pomyli to tez zostanie zrugany (on sam bledu nie wylapie
.
Omikron tez musi uwazac
19 sie 23:40
Mila:
Sporo zachodu, to prawda. Jednak na pierwsze ćwiczenie chyba dobre.
Wzór oczywiście jest w tablicach.
Jutro inne wzory wezmę z tablic, aby przećwiczyć.
Gorzej z tymi ciągami rekurencyjnymi, ale też mam jakieś zadania z odpowiedziami,
to będę wiedzieć do czego dążyć.
Dobranoc
19 sie 23:41
Saizou :
Powodzenia w liczeniu
Dobranoc
Milu
19 sie 23:44
Benny: @Saizou
Zaburzanie sum?
19 sie 23:44
6latek : A co trzeba umiec do tych funkcji tworzacych ?
19 sie 23:45
Saizou :
Żeby tylko sum
Tak się zastanawiam czy nie pisać pracy lic o szeregach
19 sie 23:51