Oblicz pole trójkąta o bokach 5.7.9 Piotr: Oblicz pole trójkąta o bokach 5.7.9 p= 5+7+9/2=10,5 teraz mam obawę czy można liczyć mając taką liczbę jak 10,5 czy to jest błąd w poleceniu wzór herona : P= (10,5−5)*(10,5−7)*(10,5−9)=28,8

Jerzy: Nie ma błędu.To połowa obwodu i nie musi byc liczbą naturalną.

Piotr: a czy wynik jest dobry?

Piotr: ?

Jerzy: Nie ... źle zastosowałeś wzór Herona

Piotr: mógłbyś obliczyć przejrzę sobie to

Jerzy: Napisz wzór Herona

Piotr: p=p(p−a)(p−b)(p−c) to wszystko pod pierwiastkiem

Jerzy: a popatrz co Ty napisałeś

Piotr: p=10,5(10,5−5)(10,5−7)(10,5−9)= p=10,5(5,5)(3,5)(1,5) teraz to wszystko mnożę i zapisuje w pierwiastku o ile idzie?

Piotr: chodzi mi że nawiasy tylko wymnażam

Janek191: P = √p*(p − a)*(p − b)*(p − c)

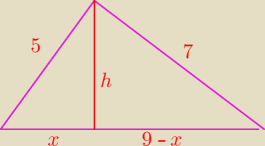
Janek191: Mamy x² + h² = 25 ( 9 − x)² + h² = 49 −−−−−−−−−−−−−−−−−−−−−− x² + h² = 25 81 − 18 x + x² + h² = 49 odejmujemy stronami −−−−−−−−−−−−−−−−−− 18 x − 81 = − 24 18 x = 57

	1		19
x = 3		=
	6		6

więc

	19
(		)2 + h2 = 25
	6

	361
h2 = 25 −
	36

	539
h2 =
	36

	√539
h =
	6

−−−−

	√539
P = 0,5* 9*		= 0,75 √539
	6

============================

Piotr: mógłbym wiedzieć skąd się wzięła liczba h² = 539/36 ?

Piotr: ?

Jerzy:

	361		900 − 361		539
25 −		=		=
	36		36		36

Piotr: tak mam zawsze liczyć pole trójkąta o danych bokach?

Piotr: ?

Piotr: jak znam miary boków np. 6.8.2 to czy zawsze mam tak liczyć?

ZKZ: ja bym tak liczyl

Jerzy: Możesz stosować wzór Herona, tak jak chciałeś

Piotr: pokaż mi jak by to wyglądało jak byś skorzystał ze wzoru herona

ZKZ: Przeciez sam mozesz podstawic w czymproblem ?

Jerzy: Nie istnieje trójkąt o takich bokach

Jerzy: 6 + 2 = 8 ... niespełniony warunek istnienia trójkąta

Piotr: Oblicz pole trójkąta o wierzchołkach A= (5,2) B=(3,0) C=(−3,6) można to szybciej zrobić czy trzeba zrobić rysunek mi wyszło że pole = 6

maciu: a przepraszam,że się wtrące,czy tego typu zadania mogą się pojawić na maturze podstawowej?

ZKZ: Moga

Piotr: pomoże ktoś z tym zadaniem Oblicz pole trójkąta o wierzchołkach A= (5,2) B=(3,0) C=(−3,6) P=6

Piotr: ?

Omikron: Możesz np. policzyć boki i wzór Herona

Omikron: Możesz policzyć bok BC i odległość punktu A od prostej BC − to będzie wysokość. Możesz ze wzoru, w którym wykorzystujesz wektory AB i AC

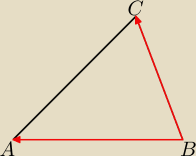
bratpik: wektor BA = [2, 2] wektor BC = [−6, 6]

	1
Pole trójkąta P =		*|2*6 − (−6*2)| = 12
	2

	1
albo po zauważeniu, że trójkąt jest prostokątny pole P =		*|AB|*|BC|
	2

Mila: Δ: 5,7,9

	5+7+9		21
p=		=
	2		2

P_Δ=√²¹₂*(²¹₂−5)*(²¹₂−7)*(²¹₂−9)= √²¹₂*¹¹₂*⁷₂*³₂=

	√21*11*21		21√11
=		==
	4		4