Zilustruj zbiór wszystkich pkt na plaszczyznie. Tomek: Moglby ktos wytlumaczyc na prostym przykladzie np xy=2y?

Omikron: xy=2y 2y−xy=0 y(2−x)=0 y=0 ⋁ 2−x=0 y=0 ∨ x=2 Rysujesz w układzie współrzędnych te dwie proste.

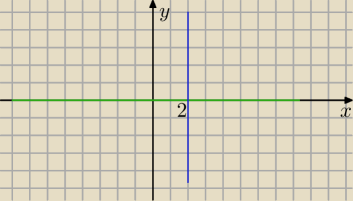
Eta: xy−2y=0 y( x−2)=0 y=0 lub x=2 zbiór punktów leżących na tych prostych np: (2,4) (2,−3) , (−2,500), .... ( −2,0) , ( 4,0) , (100,0) .....

Eta:

Omikron:

Eta:

Tomek: Dziekuje.

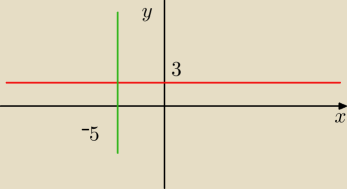
Tomek: A propos przykladu (x+5)(y−3)=0 wg. mnie powinno byc tak jak na rysunku a wg. ksiazki y=3 i x=−3. Błąd w książce?

Eta: y= 3 lub x= −5 ( spójnik i jest błędnym zapisem a*b=0 ⇔ a=0 lub b= 0

Tomek: Dziękuję Rzeczywiście nie pomyślałem o tym, gdy pisałem .

Eta: Na zdrowie ...

Tomek: A wie ktoś może jakie musząc byc założenia tutaj? |y−x|=x? wyjdzie y=2x lub y=0 tylko nie wiem czemu w 1 cwiartce. Wiem, że takie |x|+|y|=3 rozpatruje sie na kazdej cwiartce, ale tego wlasnie nie jestem pewniem probowalem y−x≥0 i y−x<0 Ale nawet jesli sa one dobre to nie wiem potem jak to zinterpretowac

Omikron: |y−x|=x Z lewej strony równania masz liczbę nieujemną, więc żeby miało ono rozwiązania, to prawa strona też musi być nieujemna. Czyli założenie to x≥0 Teraz alternatywa rozwiązań. y−x=x ⋁ y−x=−x y=2x ∨ y=0 Rysujesz w takim razie te dwie proste, ale tylko dla x≥0, co w tym przypadku sprowadza się do pierwszej ćwiartki. Twoim sposobem musiałbyś wziąć pod uwagę proste y≥0 i y<0 Sprawdzasz kiedy prosta y=2x jest ponad prostą (lub w tym samym punkcie) y=x i dla tego przypadku rysujesz. Sprawdzasz kiedy prosta y=0 jest poniżej prostej y=0 i dla tego przypadku rysujesz.

Omikron: Błąd na początku drugiego akapitu, chodzi oczywiście o prostą y=x

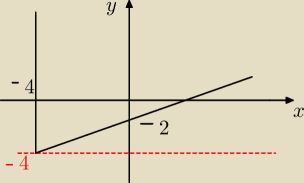
Tomek: Hmm ciekawe czyli dla np. rownania |x−y|−y=4 Mamy: |x−y|=4+y zał. 4+y≥0⇔y≥4 x−y=4+y v x−y=−4−y => x=−4 x=2(2+y)

x
	−2=y
2

Tomek: Oczywiście założenie powinno byc y≥−4, zapomnialem o minusie

Omikron: Tak

Tomek: Ok. Dzieki za pomoc

Omikron: Proszę