Planimetria. Ona147: Zadania: http://i.imgur.com/jXvPNEM.png

Jerzy: Wskazówka do zad. 5) Mając bok trójkąta, wyliczysz jego wysokość h

	1
Promień okręgu wpisanego: r =		h
	3

	2
Promień okręgu opisanego: R =		h
	3

Eta:

	a√3
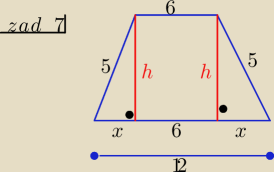
zad5/ a=12 to h=		⇒ h= 6√3
	2

h=3r ⇒ 3r=6√3 ⇒ r=2√3 R=2r ⇒ R=4√3 P_kwp= πr² = π(2√3)² = 12π P_kop=πR² = π(4√3)²= 48π zad6/ z twierdzenia Pitagorasa c²=15²+8² ⇒ c= 17

	c
ze wzorów : R=		=
	2

	a+b−c
r=		=.....
	2

zad7/ x= (12−6) :2 ⇒ x= 3 z twierdzenia Pitagorasa h²= 5²−3² ⇒ h=.....

	a+b
P=		*h=......
	2

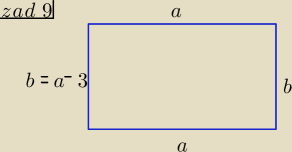Eta: zad 9/ b= a−3 , a∊(0,3) Obwód : 2a +2b = 40 to a+b= 20 ⇒ a+a−3=20 2a= 23 ⇒ a= 11,5 to b= a−3 ⇒ b= 8,5 zad10 / A( −1,2) , B(3,4) |AB|= √(x_B−xA)²+(y_B−y_A)²= ......

	xA+xB		yA+yB
S(		,		)= S(......, .......)
	2		2

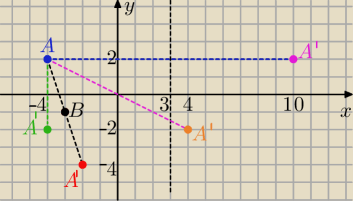Eta: zad, 11/ a) A( x,y) → S_Ox → A^'(x, −y) to A^'( −4,−2) b) A(x,y) → S_x=a → A^'( 2a−x,y) to A^'(10,2) c) A(x,y) → S_(0,0) → A^'(−x,−y) to A^'( 4,−2) d) A(x,y) → S_B(a,b) → A^'( 2a−x, 2b −y) to: A^'( −6+4, −2−2) = (−2, −4)