licea oglonoksztalcace (1974r)
6latek : Omikron 
sam ocenisz ale wydaje mi sie ze uczniowie z rozszserzenia nie powinni mie z tym problemow
Zadnie nr 1
dana jest parabola y
2=8x i jej punkty A(2,4) i B(2,−4)
W pole ograniczone parabola i odcinkiem AB wpisano prostokat
Zbadac zaleznosc pola S tego prostokata od odcietych jego wierzcholkow lezacych na paraboli
zadanie nr 2
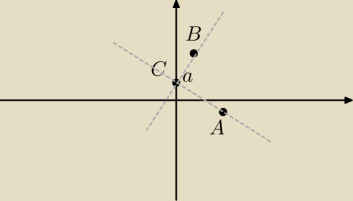
dane sa punkty a(6,−1) b(2,6)
Obliczyc rzedne punktow C na osi OY spelniajacych warunek
| | 1 | | 1 | |
∡ACB= |
| π b) ∡ACB > |
| π. |
| | 2 | | 2 | |
Zadanie nr 3
Rozwiaz nierownosc
| | 2x−1 | |
logx |
| >1 (wedlug mnie to latwe |
| | x−1 | |
Zadanie nr 4
10 ksiazek wsrod ktorych znajduja sie Potop , Wierna rzeka , Pan Tadeusz (nie wodka)
ustawiono wsposob losowy na pustej polce
Obliczyc pradopodobienstwo zdarzenia
a) Wierna rzeka , Pan tadeusz i Potop znajduja sie obok siebie
b) Potop i Wierna rzeka stoja obok siebie natoniast Pan T
adeusz nie sasiaduje z zadna z nich .
ZAdanie nr 5
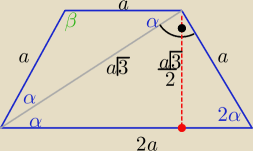
Stosunek dlugosci podstaw trapezu rownoramiennego jest 2:1
Przekatna tego trapezu polowi kat pomiedzy dluzsza posdtawa a a ramieniem
Obliczyc dlugosci bokow i miary katow trapezu wiedzac ze jego pole jest rowne S
Masz 3 zadania do wyboru .
13 sie 15:50
6latek : Pozniej napiszse ci zadnia na egzaminy na studia matematyczne
Teraz boli mnie reka

13 sie 15:52
Omikron: Popatrzę na te zadania jak do domu wrócę, dzięki.
13 sie 15:53
Eta:
Zad 5)
Odp : miary kątów : 60
o,60
o, 120
o, 120
o
| | 4 | | 2 | |
długości podstaw: |
| √S√3 , |
| √S√3 |
| | 3 | | 3 | |

13 sie 16:07
6latek : Eta 
To wyglada na poziom rozszserzony?
Oprocz zadania nr 1 gdzie ta parabole nalezy narysowac inaczej to powinni dac rade
13 sie 16:19
Jack: zad 5. mi tak samo wyszlo (dlugosci podstaw) jednakze jak katy wyznaczyc to nie wiem ; D
btw.
Witaj 5latku

13 sie 18:59
6latek : Witaj
Jack 
13 sie 19:01
uuu: Trójkat wyznaczony przez ramię, krótszą podstawę i przekatną jest trójkatem równoramiennym.
13 sie 19:05
Eta:
13 sie 19:05
Jack: dobra, niech bedzie : D
Pitagorasa trzeba bylo i odrazu wiadomo ;
13 sie 19:09
Metis: Dwa razy Pitagorasem

13 sie 19:10
Eta:

.... ja lubię trójkąt "ekierkę"
13 sie 19:12
6latek : Omikron
jesli ktos chcial isc na matematyke (studia uniwersytekcie) to w 1974 r musial sie zmierzyc z
takimi zadaniami
zadanie nr 1
Szescian ktorego krawedz na dlugosc l przecieto plaszczyzna ktora przechodzi przez krawedz
podstawy i tworzy z podstawa kat x
Wyrazic pole y przekroju i sporzadzic wykres y jako funkcji x
Wyznaczyc wartosci ekstermalne
Zadanie nr 2
Liczby (−1) ,0 1 sa pierwiastkami wielomianu o wspolczynnikach calkowitych . Wykazac z
ewartosc tego wielomianu dla dowolnej liczby calkowitej jest podzielna przez 6 .
Zadanie nr 3
Okregi o promieniach r i R gdzie r<r sa styczne wewnetrznie a ich srodki naleza do prostej
k.
Niech x oznacza odleglosc punktu stycznosci od prostej m prostopadlej do k i przecinajacej
okregi
Wyrazic stosunek dlugosci cieciw obu okregow zawartych w prostej m w zaleznosci od x>0
Obliczys granice tego stosunku gdy x→0.
Zadanie nr 4
Losowo ustawia sie w ciag n ludzi wsrod ktorych sa osoby A i B .
jakie jest prawdopodobienstwo ze miedzy A i B stanie dokladnie r ludzi?
Zadanie nr 5
dany jest dowolny czworokat plaski
Ile elementow moze miec zbior wszystkich izometrii przeksztalcajacych ten czworokąt na siebie ?
czas trwania 4 godziny
13 sie 19:16
frab: Skad ty 6latek to wszystko wiesz?
13 sie 19:33
Eta:
pasjonat 
13 sie 19:37
frab: Ale chodzi mi o takie stare! Starsze o wiele ode mnie

13 sie 19:42
6latek : frab
Np Zbior zadan z matematyki dla kandydatow na wyzszse uczlnie techniczne B Gdowski . E
Plucinski
ja mam z 1976r (sa nowsze wydania
13 sie 19:51
frab: Skąd ty masz takie zbiory
13 sie 19:58
Omikron:

To może od trzeciego zacznę.
Zad 3
Najpierw dziedzina.
| | 2x−1 | |
D= {x:x∊R∧x>0∧x≠1⋀ |
| >0} |
| | x−1 | |
(2x−1)(x−1)>0
| | 1 | |
Ostatecznie D=(0, |
| )∪(1,∞) |
| | 2 | |
| | 1 | |
I teraz dwa przypadki, pierwszy to x∊(0, |
| ), wtedy mamy do czynienia z funkcją malejącą |
| | 2 | |
czyli zmieniamy znak przy opuszczaniu logarytmu.
(2x−1−x
2+x)(x−1)>0
(x
2−3x+1)(x−1)<0
Δ=5
x
3=1
| | 3−√5 | |
Biorąc pod uwagę dziedzinę x∊(0, |
| ) |
| | 2 | |
Drugi przypadek x∊(1,
∞), wtedy funkcja rosnąca, nie zmieniam znaku.
Wszystko to samo, tylko na końcu >0
Ostatecznie
| | 3−√5 | | 3+√5 | |
x∊(0, |
| )∪( |
| ,∞) |
| | 2 | | 2 | |
Zad 4
|Ω|=10!
a) Ustawienie obok siebie może być na 8 sposobów, oprócz tego ustawienie względem siebie na 3!
sposobów. Pozostałe na 7! sposobów.
|A|=3! * 7! * 8
b) Rozrysowałem sobie i wyszło mi 112 możliwości ułożenia książek względem siebie i tej
trzeciej. Pozostałe na 7!
|B|=112* 7!
Zad 5
Z sumy kątów wyszło mi, że trójkąt DCA jest równoramienny, więc |AD|=|BC|=x
Z Pitagorasa
| | 2 | |
I dalej już łatwo, podstawiam do |
| S=hx, a kąty obliczę z sinusa w którymś trójkącie |
| | 3 | |
prostokątnym.
Jeszcze nad tymi dwoma pomyślę, a w tych co zrobiłem, mam nadzieję, że błędów nie ma.
13 sie 20:02
13 sie 20:02
6latek :
Zadanie nr 4 dobrze
Zadnie nr 5 wiesz jakz robic
Zadanie nr 3 zle
| | 3−√5 | | 1 | | 3+√5 | |
x∊( |
| , |
| )U(1, |
| ) |
| | 2 | | 2 | | 2 | |
13 sie 20:09
uuu: Zad 2
W(x)=g(x)x(x−1)(x+1) −trzy kolejne liczy całkowite bedą zawsze dla x− całkowitego więc albo
bedzie 0 albo zawsze +−2 i +−3
13 sie 20:09
13 sie 20:13
uuu: Zad 3
S=√(2R−x)/(2r−x)
Granica=√R/r
13 sie 20:22
Omikron: W trzecim napisałem, że zmieniamy znak po opuszczeniu logarytmu i nie zmieniłem znaku

13 sie 20:23
frab: Czy w zad 1 przekrój nie zalezy od tego jakim kątem jest x? bo raz moze być trójkatem 0<x≤45
lub czworokatem x>45 i x≤90
13 sie 20:36
Omikron:
Zad 2
A(6,−1)
B(2,6)
C(0,c)
a) Kąt ma być 90 stopni.
Najpierw znajdę równania prostych.
AC:
−1=6a+b
c=b
Odejmuję stronami
−1−c=6a
BC:
6=2a+b
c=b
6−c=2a
I teraz warunek prostopadłości.
(18−3c)(−1−c)=−6
Dalej prosto.
W podpunkcie b wykorzystałbym wzór na tangens kąta między prostymi i stwierdziłbym, że musi być
ujemny.
Wzór musiałem sprawdzić, ale na swoją obronę powiem, że na maturze go pamiętałem

13 sie 20:37
13 sie 20:44
uuu: | | 8*3!*7! | |
Wg mnie chyba tak P(A)= |
| |
| | 10! | |
13 sie 20:47
uuu: Zad 4
b) A=2(7*7!*2+6*7*7!)
Ω=10!
13 sie 20:52
Omikron:
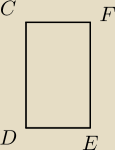
Zad 1
Jako c oznaczyłem odciętą wierzchołka na paraboli. Wtedy rzędna to 2
√2c.
Wyliczyłem boki i wyszło mi coś takiego:
Dziedzina c to (0,2)
C=(c,2
√2c)
D=(c,−2
√2c)
E=(2,−2
√2c)
F=(2,2
√2c)
|CD|=4
√2c
|DE|=2−c
S=4
√2c*(2−c)
Nie jestem jednak pewny czy nie trzeba było zrobić czegoś innego, bo po raz pierwszy spotykam
się z taką "inną parabolą".
Dużo geometrii, ale musieliście zrobić 3 z 5 zadań, więc jeżeli czegoś nie umieliście to wciąż
mogliście mieć max punktów.
Na wstępnych egzaminach też były 3 zadania do wyboru?
13 sie 21:17
6latek : Nic nie piszse ze do wyboru
13 sie 21:21
Omikron: To tutaj gorzej. Jak znajdę trochę czasu to pomyślę nad tymi zadaniami dzisiaj, jak nie to
zajmę się nimi jutro.
13 sie 21:34
uuu: Czy moje odp są poprawne?
13 sie 21:35
frab: Zad 5
Najwiecej chyba bedzie miał kwadrat bo 8?
14 sie 08:32
6latek : uuu i
frab
Odpowiedzi mam takie do 2 zestawu
zad3
Zad 5 1,2, 4, 8
14 sie 09:19
uuu: Czyli Zad 3 i 4 mam dobrze. A zadanie 2 jest OK?
Zad 5
8 −kwdarat
4−prostokąt, romb
1 i 2 to nie wiem

14 sie 09:33
frab: Czy w zad 1 przekrój nie zalezy od tego jakim kątem jest x? bo raz moze być trójkatem 0<x≤45
lub czworokatem x>45 i x≤90 i x=0

14 sie 09:34
uuu: Zad 5
1 − to tożsamość a który czworokat ma 2?
14 sie 09:37
uuu: Czy to bedzie symetria wzgledem punktu przeciecia przekatnych w rownolegloboku?
14 sie 09:39
6latek : Nie ma do zadania nr 1 i2 wiec musicie sami dojsc sobie
Jet mi trudno pisac ale napiszse jeszce wam
Studia techniczne Wariant A
czesc 1 (czas trwania 2 godziny )
Na hiperboli x
2−y
2=a
2 obrano dowolny punkt w 1 cwiartce plaszczyzny Przez ten punkt
poprowadzono dwie rozne proste , z ktorych kazda zawiera jeden z wierzcholkow hiperboli
Wykazac ze suma katow ostrych jakie te proste tworza z osia X jest katem prostym
Zadanie nr 2
dane jest rownanie kwadratowe
mx
2−(m
2+1)x+m
2+1=0
Zbadac sume pierwiastkow rzeczywistych tego rownania jak funkcji parametru m i podac wykres tej
funkcji (latwizna )
Zadanie nr 3 W dwoch naczyniach znajduja sie roztwory soli o roznych stezenianaich , w
pierwszym m kg a w drugim n kg . Z kazdego naczynia pobrano taka sama ilosc roztworu a
nastepnie przelano do drugiego z naczyn .
Wtedy okazalo se ze stezenia procentowe roztworow w obu naczyniach sa jednakowe.
ile kg roztworu pobrano z kazdego naczynia ?
Czesc druga (3 zadania do wyboru czas trwania 2,5 godziny)
Zadanie nr 1
W trojkacie ABC boki AC i BC sa rowne
Okrag ktorego srednica jest wysokosc CD trojkata przecina boki trojkata w punktach dzielacych
te boki w stosunku mdo n liczac od wierzcholka C
Obliczyc pole trojkata ABC majac dana wysokosc CD rowna a
zadanie nr 2
jeden z bokow trojkata lezy na plazcyznie P
Pozostale boki tworza z plaszczyzna P katy α i β a rzuty tych bokow na plaszcyzne P sa
prostopadle
Znalezc tangens kata nachylenia plaszczyzny trojkata do placzyzny P
ZAdanie nr 3
Oblicz wartosc wyrazenia
−1+2−3+.....(−1)
nn
ZAdanie nr 4
Dla jakich wartosci x∊<0,π> spelniona jest nierownosc
Ostatnie juz
Nr 5
SPosrod 20 mezczyzn i 5 kobiet wybrano 3 ososbowa delegacje
Zakaldamy z ekazda osoba miala te sama szanse wyboru
Obliczyc prawdpodobienstwo ze w sklad delegacji weszla conajmniej jedna kobieta .
14 sie 09:46
6latek : Moze dopytajcie Panowie Ete albo Mile lub tez moze pojawi sie Qulka
One sa na biezaco z tym (tak mi sie wydaje .
14 sie 09:52
uuu: Geometria
zad1
Mi wyszło pole (m+n)*√mn
14 sie 10:04
uuu: Zad 2
Wg mnie to jest ostrosłup o wysokości która jest jego krawadzią(H). A dwie sciany boczne sa
trójkatami prostokatnymi. Wysatrczy policzyć wysokość tego trójkata i wysokość podstawy
uzaleznione od H.
14 sie 10:21
14 sie 10:22
6latek : Masz odp do 2 zestwu
nr 1 juz napisalem
nr 2
√tg2α+tg2β
nr 3
Nr 4
| | 1 | | 1 | | 1 | | 3 | |
x∊( |
| π, |
| π)U( |
| π, |
| π) |
| | 4 | | 3 | | 2 | | 4 | |
Moze takze kolega skorzysta
14 sie 10:29
maciu : ja nie umiem zadnego
14 sie 10:56
Omikron: Z tego co widzę z geometrii trudne zadania, ale spróbuję je później zrobić.
14 sie 11:40
farb: zad1 CD jest średnicą okręgu, więc trójkąty: ADC, ADE, DEC są prostokątne i tu trzeba
skorzystać h2=x*y i pare razy tw Pitagorasa
14 sie 12:05
6latek : farb z jakiego wojewodzta jetes?
14 sie 12:35
farb: łodzikie a czemu
14 sie 12:37
6latek : Tak z ciekawosci zapytalem .
Matura 1964r (Lodz miasto)
Wedlug mnie latwa
Zadanie nr 1
W ostroslupie SABC wpisamym w stozek podsatwa ABC jest trojkatem rownoramiennym o ramionach
AB=AC=a i kacie miedzy nimi zawartym α
Obliczyc objetosc stozka jesli sciana boczna BSC jest nachylona do plaszcyzny podstawy pod
katem β.
Wykonac obliczenia dla a= 34,67
α=42o43'
β=56o17'
Zadanie nr 2
Suma trzech liczb tworzacych ciag geomwetryczny wynosi 62
SUma zas ich logarytmow jest rowna 3 Znalezc te liczby
Zadanie nr 3
Rozwiazac rownanie
sin4x−cos4x= 0,25(sinx+cosx)2
14 sie 12:48
6latek : Rysunek do zadania nr 1 musisz oczywisci wykonac sam bo wtedy nie robiono rysunkow do zadania
(kazdy musial sobie zrobic sam
14 sie 12:59
Omikron: Spróbuję teraz zrobić drugi zestaw zadań (ten na studia uniwersyteckie).
Zad 1
Przekrój jest prostokątem o jednym boku l i drugim nieznanym. Ten nieznany bok jest
przeciwprostokątną trójkąta prostokątnego, jego przyprostokątną jest l, a kątem przy l jest x.
Nieznany bok oznaczam jako w.
Dalej nic nie zrobię, bo pochodna z funkcji trygonometrycznych to teraz poziom studiów.
Zad 2
W(x)=a(x−1)x(x+1) ∧ a∊C ⋀ x∊C
Iloczyn trzech kolejnych liczb całkowitych podzielny przez 6
c.k.d.
Zad 3
Rozrysowałem sobie i rozwiązanie sprowadza się do zastosowania dwa razy Pitagorasa. W jednym
przypadku mamy trójkąt w (mała cięciwa), x, r−x.
W drugim przypadku trójkąt z (duża cięciwa), R, R−x
Wychodzi ostatecznie
Zad 4
|Ω|=n!
Co do A, popełniłem błąd, ale po sprawdzeniu odpowiedzi wiem dlaczego powinno wyjść jak jest.
(n−r−1) − to jest możliwość sztywnego ustawienia grupy A, r osób, B
2 − możliwość przestawienia miejscami A i B
(n−2)! − możliwości postawienia na konkretnych miejscach wszystkich osób poza A i B
|A|=2(n−r−1)*(n−2)!
Zad 5
Tutaj nie wiem czy powinienem jakoś udowodnić dlaczego, czy po prostu stwierdzić, dziwne się to
zadanie wydaje.
W większości te zadania nie są bardzo trudne, ale myślę, że na wyższym poziomie niż matura
teraz. "Myślę", ale nie jestem przekonany czy można to porównywać, bo jednak wtedy byliście
przygotowywani do tej innej matury, a w programie nauczania liceum było więcej.
14 sie 19:58
Benny: W zadaniu drugim nie ma żadnej informacji, że wielomian jest trzeciego stopnia.
14 sie 20:05
Omikron: Nie ma, ale poza tym, że powinienem inaczej zapisać wzór wielomianu (wykropkować?) to nic nie
zmienia.
14 sie 20:06
Benny: W(x)=x(x−1)(x+1)Q(x)
14 sie 20:07
Omikron: No tak, tak najłatwiej
14 sie 20:19
frab: Jak ty rozwiązałes zadane 1? Czy w zad 1 przekrój nie zalezy od tego jakim kątem jest x? bo
raz moze być trójkatem 0<x≤45 lub czworokatem x>45 i x≤90 i x=0
14 sie 20:27
Omikron: Jakby był trójkątem, to nie byłby to przekrój, bo nie dzieliłby sześcianu na dwie części
(pomiędzy tymi częściami byłoby połączenie).
14 sie 20:28
frab: Nadal nie rozumiem twojego toku myslenia.
14 sie 20:38
frab: Czemu to nie moze być np trapez?
14 sie 20:42
Omikron:
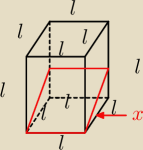
W jaki sposób to, jaką figurą jest przekrój, zależy od miary x?
14 sie 20:43
 sam ocenisz ale wydaje mi sie ze uczniowie z rozszserzenia nie powinni mie z tym problemow
Zadnie nr 1
dana jest parabola y2=8x i jej punkty A(2,4) i B(2,−4)
W pole ograniczone parabola i odcinkiem AB wpisano prostokat
Zbadac zaleznosc pola S tego prostokata od odcietych jego wierzcholkow lezacych na paraboli
zadanie nr 2
dane sa punkty a(6,−1) b(2,6)
Obliczyc rzedne punktow C na osi OY spelniajacych warunek
sam ocenisz ale wydaje mi sie ze uczniowie z rozszserzenia nie powinni mie z tym problemow
Zadnie nr 1
dana jest parabola y2=8x i jej punkty A(2,4) i B(2,−4)
W pole ograniczone parabola i odcinkiem AB wpisano prostokat
Zbadac zaleznosc pola S tego prostokata od odcietych jego wierzcholkow lezacych na paraboli
zadanie nr 2
dane sa punkty a(6,−1) b(2,6)
Obliczyc rzedne punktow C na osi OY spelniajacych warunek


 To wyglada na poziom rozszserzony?
Oprocz zadania nr 1 gdzie ta parabole nalezy narysowac inaczej to powinni dac rade
To wyglada na poziom rozszserzony?
Oprocz zadania nr 1 gdzie ta parabole nalezy narysowac inaczej to powinni dac rade




 .... ja lubię trójkąt "ekierkę"
.... ja lubię trójkąt "ekierkę"


 To może od trzeciego zacznę.
Zad 3
Najpierw dziedzina.
To może od trzeciego zacznę.
Zad 3
Najpierw dziedzina.

 Zad 2
A(6,−1)
B(2,6)
C(0,c)
a) Kąt ma być 90 stopni.
Najpierw znajdę równania prostych.
AC:
−1=6a+b
c=b
Odejmuję stronami
−1−c=6a
Zad 2
A(6,−1)
B(2,6)
C(0,c)
a) Kąt ma być 90 stopni.
Najpierw znajdę równania prostych.
AC:
−1=6a+b
c=b
Odejmuję stronami
−1−c=6a

 Zad 1
Jako c oznaczyłem odciętą wierzchołka na paraboli. Wtedy rzędna to 2√2c.
Wyliczyłem boki i wyszło mi coś takiego:
Dziedzina c to (0,2)
C=(c,2√2c)
D=(c,−2√2c)
E=(2,−2√2c)
F=(2,2√2c)
|CD|=4√2c
|DE|=2−c
S=4√2c*(2−c)
Nie jestem jednak pewny czy nie trzeba było zrobić czegoś innego, bo po raz pierwszy spotykam
się z taką "inną parabolą".
Dużo geometrii, ale musieliście zrobić 3 z 5 zadań, więc jeżeli czegoś nie umieliście to wciąż
mogliście mieć max punktów.
Na wstępnych egzaminach też były 3 zadania do wyboru?
Zad 1
Jako c oznaczyłem odciętą wierzchołka na paraboli. Wtedy rzędna to 2√2c.
Wyliczyłem boki i wyszło mi coś takiego:
Dziedzina c to (0,2)
C=(c,2√2c)
D=(c,−2√2c)
E=(2,−2√2c)
F=(2,2√2c)
|CD|=4√2c
|DE|=2−c
S=4√2c*(2−c)
Nie jestem jednak pewny czy nie trzeba było zrobić czegoś innego, bo po raz pierwszy spotykam
się z taką "inną parabolą".
Dużo geometrii, ale musieliście zrobić 3 z 5 zadań, więc jeżeli czegoś nie umieliście to wciąż
mogliście mieć max punktów.
Na wstępnych egzaminach też były 3 zadania do wyboru?


 W jaki sposób to, jaką figurą jest przekrój, zależy od miary x?
W jaki sposób to, jaką figurą jest przekrój, zależy od miary x?