o
maciu: podstawą ostroslupa prawidlowego czworokatnego ABCDS jest kwadrat ABCD wszystkie sciany boczne
tego ostroslupa sa trojkatami rownobocznymi ,miara kata ACS jest rowna ile? czy to zadanie
jest łatwe czy raczej jedno z trudniejszych?noi prosze mi to wytłumaczyc
12 sie 14:42
Janek191:
Jakimi trójkątami są ściany boczne ostrosłupa ?
12 sie 14:48
Janek191:
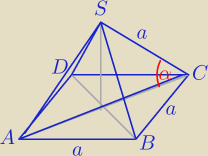
12 sie 14:52
maciu: nie jest podane w zadania,jaśniej prosze ten rysunek nic mi nie mowi

12 sie 14:54
Janek191:
I AC I = a
√2 ⇒ x = 0,5 I A C I = 0,5 a
√2
| | x | | 0,5 a √2 | | √2 | |
cos α = |
| = |
| = |
| |
| | a | | a | | 2 | |
więc
α = 45
o
12 sie 14:55
maciu: a co to jest a√2 i skad to sie wzięło?
12 sie 14:56
Janek191:
Długość przekątnej kwadratu ABCD o boku długości a.
I AC I = a√2
12 sie 14:59
maciu: to raczej trudne zadanie
12 sie 15:02
Smule:

| | OC | | 0.5*a√2 | | √2 | |
cosα = |
| = |
| = |
| |
| | SC | | a | | 2 | |
w takim razie α = 45 stopni
12 sie 15:02
Smule: to latwe zadanie ale jak sie nie potrafi podstaw geometrii na plaszczyznie z gimnazjum to nie
zrobisz zadnego zadania z geometrii w przestrzeni
12 sie 15:04
Smule: geometria w przestrzeni to glownie twierdzenie pitagorasa i trygonometria, ale ty chyba tego
nie umiesz
12 sie 15:06
maciu: umiem pitagorasa trygonometrie też

12 sie 15:12



