Pomoże ktoś obliczyć 'h'. Nie jestem w stanie nic wymyślić Z góry dzięki. Mati: http://www.tinypic.pl/szyhwcyjab8i

maciu: Ja tego nie pojmuje

Mariusz: Po dwukrotnym skorzystaniu z twierdzenia Pitagorasa mamy 2yh+h²=c²−d² Z trygonometrii wiemy że y=1340sin(34.4°) Pozostaje tylko obliczyć przeciwprostokątne c oraz d

Mariusz: Po skorzystaniu z twierdzenia cosinusów otrzymujemy h²=c²+d²−2cd cos(58.8°) Mamy zatem układ równań 2yh+h²=c²−d² h²=c²+d²−2cd cos(58.8°) y=1340sin(34.4°) i brakuje nam jeszcze jednego równania

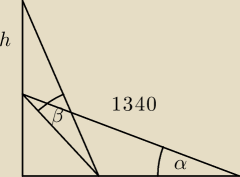
Mariusz: α=34.4° β=58.8°

Mariusz: Zastanawiam się czy dane są poprawne Trójkąty zawierające interesujące nas przeciwprostokątne mają być rozwartokątne ponieważ współczynniki kierunkowe prostych zawierających interesujące nas przeciwprostokątne są ujemne więc tangens kąta nachylenia jest ujemny a co za tym idzie kąt nachylenia musi być rozwarty Już suma dwóch kątów przekraczałaby 180 γ>34.4+90+58.8 γ>183.2 Na sferze jest nadwyżka sferyczna ale twierdzenie cosinusów jest trochę inne Twierdzenie Pitagorasa można traktować jako przypadek szczególny twierdzenia cosinusów