trójkat trojnik: ABC jest trójkątem o bokach a,b,c. R jest promieniem ookregu opisanego. Jak wykazac ze 2 min(|a−b|,|b−c|,|c−a|) ≤ R

g:

	α
a = 2R sin
	2

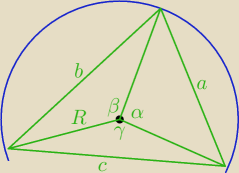
	γ		β
c−b = 2R (sin		− sin		)
	2		2

	β		α
b−a = 2R (sin		− sin		)
	2		2

Zakładam że a < b < c. W rachubę wchodzą (c−b) i (b−a). Jeśli ustalimy R,c,γ i tak dobierzemy a i b, żeby (c−b) = (b−a) to wtedy min(c−b, b−a) osiąga wartość maksymalną. Wystarczy udowodnić tezę dla tego przypadku, bo w innych będzie łatwiej.

	β		γ		α
(c−b) = (b−a) ⇒ 2sin		= sin		+ sin
	2		2		2

	γ		α
⇒ c−b = R (sin		− sin		) (1)
	2		2

	γ+α		γ		α
⇒ 2sin		= sin		+ sin		(2)
	2		2		2

	α		γ
Z równania (2) można wyznaczyć sin		jako funkcję sin		(trochę z tym roboty)
	2		2

	α		γ		3
sin		= sin				(3)
	2		2		γ   5 − 4cos   2

Teraz wstawiam (3) do (1)

	γ		γ   2 − 4cos   2
c−b = R sin				(4)
	2		γ   5 − 4cos   2

Wiadomo że γ > 120 (bo c jest najdłuższym bokiem). Trzeba zbadać funkcję (4) w zakresie 120 < γ < 360. Na razie zrobiłem wykres w Excelu

	1
i wyszło, że osiąga maksimum =		R dla γ ≈ 230.
	2

	1
Wniosek c−b ≤		R.
	2

jc: sin γ = − 3/4 γ = 228^o

g: A jak do tego doszedłeś?

trojnik: Czyli nie da się tego rozwiązać bez komputera?

jc: g, zróżniczkowałem. Badanie ekstremów wyrażenia (4), to dobre zadanie na egzamin. Oczywiście wcześniej narysowałem sobie wykres (ja używam gnuplota, wystarczy wpisać wzór i mamy wykres). Na zadanie z geometrii na pewno jeszcze spojrzę.

jc: Trójkąt dla którego osiągane minimum ma boki o długościach:

	R		R		R
(√7 − 1)		, √7		, (√7 + 1)
	2		2		2

jc: Źle napisałem. Jeśli a=√7+1, b=√7, c=√7−1, to 2 min(|a−b|, |b−c|, |c−a| ) = R.