trójkąt niki: Mam takie zadanie nie wiem jak sie do niego zabrać ABC jest równoramieny gdzie AB = AC = 3. Na BC obieramy k różnych punktów, oznaczmy je przez P₁, P₂, P₃...P_k. Niech X_i = (AP_i)² + (BP_i x P_iC) gdzie i = 1, 2, 3...k. Oblicz wartość k jeśli X₁ + X₂ + X₃+ ...+ X_k = 1080. Ps ten "x" oznacza mnozenie.

niki: Czy ktoś to umie?

Mila: x_i=3²=9

niki : nie rozumiem

niki: Mila co miałas na mysli ?

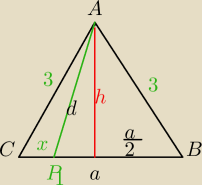
Mila: |BC|=a

	a
h2+(		)2=9
	2

	a2
h2=9−
	4

	a2		a2
d2=h2+(a/2−x)2=9−		+		−ax+x2
	4		4

	a2		a2
x1=d2+(a−x)*x=9−		+		−ax+x2+ax−x2
	4		4

x₁=9 niezależnie od wyboru punktu P_i x_i=9 k*9=1080

niki: Dzieki przeanalizuje i jakby co zapytam

Mila: A masz odpowiedź? Z jakiego to zbioru?