Roznowartosciowa i jednoznaczna 6latek: Funkcje f nazywamy funkcja roznowartosciowa jesli swoja wartosc przyjmuje tylkojeden raz tzn dla x₁≠x₂ mamy f(x₁)≠f(x₂). Funkcje roznowartosciowa odwzorujaca zbior X na zbior Y nazywamy wzajemnie jednoznaczna Wiem ze funkcja jest (na) jezeli kazdy elemnet ze zbioru Y jest wartoscia funkcji dla pewnwgo x∊X to mamy odwzorowanie (na) To wedlug mnie kazda funkcja roznowartosciowa jest funkcja wzajemnie jednoznaczna Czy moze byc inaczej Jesli tak to,proszse pokazac to ewentualnie na grafie .

6latek: To bedzie funkcja roznowartosciowa i to jest odwzorowanie (w) bo nie kazdy element zbioru Y jest wartoscia funkcji dla pewnego x_sa ze zbioru X zostal elemnet rozowy i to nie bedzie odwzorowanie wzajemnie jednoznaczne . tak mysle

jc: Spójrz jeszcze raz na trzy obrazki. X = {1}, Y={1,2}, funkcja f: X →Y taka, że f(1) = 1 jest różnowartościowa, ale nie jest bijekcją.

jc: Rozminęły się wpisy

6latek: Tutaj natomiast mamy odwzorowanie wzajemnie jednoznaczne i z tej funkcji mozemy juz wyznaczyc funkcje odwrotna tak pomyslalem Tylko to jest graf a funkcje mozna przedstawic rownieez w inny sposb . jak to rozpoznac?

6latek: Czesc jc Dla mnie wlasnie sa najgorszse te zapisy w postaci tych nawiasow klamrowych ja tego nie rozumiem

jc: {1,2,3,4} oznacza zbiór złożony z elementów 1,2,3,4. Co w tym strasznego?

6latek: No dobrze Powiedzmy ze mamy X={1,2 3 4} i Y={2,3 4} jak tutaj rozpoznac i jak rozpisac jesli chca aby byla na lub w ? Proszse wytlumacz to dokladnie

6latek: To moze byc jeden z ukladow w?

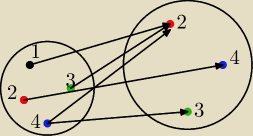
6latek: To moze byc jeden z ukladow na Teraz zadm Ci pytanie Czy ja dobrze mysle Jesli funkcja ma byc roznowartosciowa i na to ilosc elementow zbioru X musi byc taka sama jak ilosc elementow zbioru Y ?

6latek: Jest na rysunku z 21:59 zle bo bo nie moze isc strzalka do 4 do 2 bo to nie bedzie funkcja

jc: Masz 3 sytuacje. 1. po prawej stronie nic nie zostaje (w przypadku skończonych zbiorów, zbiór po lewej stronie nie może mieć mniej elementów niż zbiór po prawej stronie). 2. strzałki nie sklejają się (w przypadku skończonych zbiorów, zbiór po prawej stronie nie może mieć mniej elementów niż zbiór po lewej stronie). 3. Strzałki łączą oba zbiory w pary ((w przypadku skończonych zbiorów, oba zbiory mają tyle samo elementów). Jak odwrócimy kierunek strzałek, otrzymamy funkcję odwrotną.

6latek: Czyli opisales 3 sytuacje gdzie funkcja jest roznowartosciowa i na ?

jc: (1) funkcja "na" , (2) funkcja różnowartościowa, (3) = (1) & (2)

6latek: Dobrze . Juz lapie