Odczytywanie ilości rozwiązań Paula: Witam, mam dosyć nietypowy problem. Siedzę i myślę juz godzinę i dalej nie potrafię odczytać ilości rozwiązań z funkcji sinus. Ogólnie nie wiem, jak się za to zabrać. Mam takie zadanie: Ile rozwiązań w podanym przedziale ma poniżśze równanie w zależności od parametru m? sinx=m, (−π;3π) oraz cosx=m, <0;4π> mam rozwiązania do tych zadań, ale nie chcę bezsensu przepisywać bez zrozumienia tego. Wiem, że rysunek to podstawa, ale co dalej?

Jerzy: po prostu przesuwasz prostą y = m wzdłuż osi OY i sprawdzasz w ilu punktach przecina wykres y = sinx w podanym przedziale, w zależności od m

Paula: a dlaczego w przykładzie sinx=m, (−π;3π) ma 4 rozwiązania dla m∊(−1;0)U(0;1) ? mam zrobić poziomą linię od −1 i drugą poziomą linię od 0?

Paula: I skąd mam wiedzieć, jakie przedziały sobie wybrać?

Paula: albo dlaczego są 2 rozwiązania w przedziale <−1;1> a nie 4?

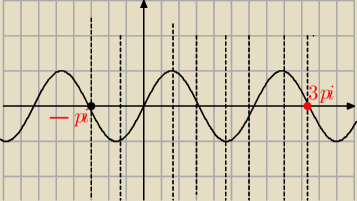
6latek: To jest wykres y=sin(x) Odczytaj z niego ile jest rozwiazanian sin(x)=0 w przedziale <−π.3π> To samo odzczytaj liczbe rozwiazan rowniania sin(x)=0 w przedziale (−π,3π) na razie tyle

Paula: dla six(x)=0 są 3 rozwiązania jeśli (−π;3) a jeśli <−π;3π> to 5 rozwiązań

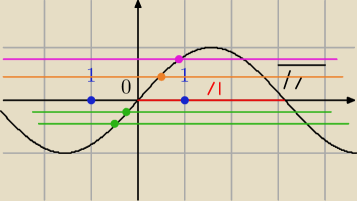
6latek: na ty samym rysunku narysuj sobie prosta y=−2 i zobacz ile jest rozwiaan w tym przedziale Tak samo sobie narysyj prosta y=1,5 i to samo . Jaki z tego wniosek ? Teraz narysuj prosta y=−5 i okresl liczbe rozwiazan w tym przedziale Potem prosta y=0,6 i okresl liczbe rozwiazan Inaczej praedstawia sie sprawa gdy chcesz napisac w przedziale <−1,1> Masz wykress y=sin(x) narysowalem go duzy zeby bylo ladnie widac Ten czerony odcinek ma dlugosc π a wiemy ze π≈3,14 wiec jeden to bedzie trzy razy mniej niz π Wiec ten odcinek dlugosci π czerwony dzielisz na trzy czesci i masz jeden U mnie akuratnie podzielilo sie ladnie Teraz naprawde masz dwa rozwiazania w tym przedziale dla sin(x)=m ?

6latek: Tak samo zrob sobie z wykresem y=cos(x)

Paula: Czyli jeśli mamy przedział to zawsze dzielimy na 3 części?

Paula: chwila, bo się pogubiłam. To <−1;1> to jest na osi X czy Y?

6latek: Tak ale w przyblizeniu dla 1

	1
masz funkcje y=sin(x) i zaznacz na nim przedzial <−2 ,		>
	2

6latek: Post 18:04 Co masz znalezc dla tego przedzialu ? Wiec na jakiej osi oznaczysz ten przedzial <−1,1> ?

Paula: zaznaczyłabym na osi Y

6latek: Inaczej Dla tego przedzialu masz znalezc ilosc rozwiazan Tak ? wiec ilosc rozwiazan na jakiej osi odczytujesz? Wiec na jakiej osi zanaczysz przedzial <−1,1> >? Na osi OX czy osi OY? Zawszse zadawaj sobie pytania . ja teraz juz musze juz zajac sie swoimi zadaniami z funkcji .

Paula: ilość rozwiązań odczytuj z osi OX

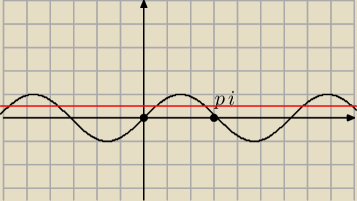
6latek: Paula mnie zalamuj mnie Przeciez ilosc rozwaizan odczytujesz na osi OY Ile jest rozwiazan dla sin(x)=0,5 w przedziale <0,pi) ? Z ktorej osi oczytujesz ?

Paula: 2 rozwiązania, odczytuję tak jakby z tej czerwonej linii czyli z osi OY?

Paula: przepraszam, jedno rozwiązanie

6latek: tak patrzysz ile razy ta czerwona linia przetnie wykres

Paula: dziękuję chyba to w końcu ogarnęłam.

6latek: Paula odpocznij sobie chwile i potem wroc do tego .Dobrze ?

6latek: W tym przedziale przetnie go 2 razy wiec sa dwa rozwiazania

Paula: ale przedział był z jednej strony otwarty w Twoim przykładzie <0 ;π)

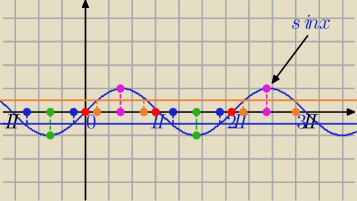
Mila: f(x)=sinx x∊(−π,3π) 1)m=0 − 3 rozwiązania 2) m=1− 2 rozwiązania 3) m=−1 −2 rozwiązania 4) m∊(0,1)− 4 rozwiązania 5) [N[m∊(−1,0) − 4 rozwiązania 6) m>1 lub m<−1 brak rozwiązań Możesz też tak: zbiorczo m∊<0,1> − 9 rozwiązań m∊<−1,0) − 6 rozwiązań.