proszę o rozwiązanie anna: dany jest wielomianu W(x)== 6x³ − 4x² liczba a jest resztą z dzielenia wielomianu w przez dwumianu x + 3 a liczba b jest resztą z dzielenia tego wielomianu przez x − 2 zakoduj cyfry setek dziesiątek i jedności liczby I 2a − b I nie wiem jak to zapisać wynik to 428

6latek: W(−3)= a W(2)= b

anna: tak też obliczyłam W(−3) = − 162 −36 = − 198 w(2) = 22 I 2a −b I = I− 396 − 22 I = 418 a wynik jest inny

Metis: W(2)=32

anna: słusznie dziękuję bardzo

Metis:

anna: liczba S jest sumą wszystkich liczb całkowitych spełniających nierówność (x² −6x +5 )(x² − 60x +500) ≤ 0 zakoduj cyfry setek dziesiątek i jedności liczby S I −wszy przypadek (x² −6x +5 ) to musi być ujemne a to (x² − 60x +500) dodatnie aby iloczyn był ujemny II − gi przypadek odwrotnie ale nadal nie wiem jak wynik to 1245 kod 245

6latek: A co z przypadkiem =0 ? Masz nierownosc slaba a nie ostra

6latek: Ja bym rozpatrywal tak 1 (x²−6x+5≤0 x²−60x+500≥0 2. x²−6x+5≥0 x²−60x+500≤0

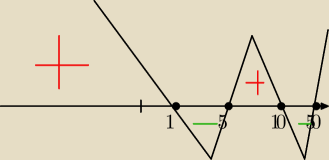
Metis: Hmmm , co wy tutaj rozpatrujecie ? Wystarczy rozwiązać (x²−6x +5)(x²−60x +500)≤0 ⇔ (x−50)(x−10)(x−5)(x−1)≤0 , stąd x∊<1,5> U < 10,50> Całkowite rozwiązania: 1,2,3,4,5 oraz 10,11,12,..., 50 Pierwszą sumę policzymy łatwo: 15 10,11,12,..., 50 ciąg art. o a₁=10, a_n=50 i r=1 S_n=1230 1230+15=1245

6latek: Metis ale

W(x)
	<0 ⇔W(x)>0 lub P(x)<0 i W(x)<0 lub P(x)>0
P(x)

tak jeszce ja rozwiazywalem takie nierownosci

6latek: Twoje rozwaizanie jest oczywiscie dobre

Metis:

anna: dziękuję bardzo