ciagłość funkcji w punkcie x0 kajka: Proszę o rozwiazanie tych dwóch przykładów Zbadaj ciągłość funkcji A) f(x)= { 3x³+7x²+5x+1/ x+1 jeśli x≠−1 0 jeśli x=−1 X0=−1 B) f (x)= { x² −x−20/x²+5x+4 jeśli x≠−4 3 jeśli x=−4 X0=−4

Jerzy: Próbuj rozkladac na czynniki jak w poprzednim przykladzie

kajka: W a mi nie wychodzi 3x³+7x²+5x+1 =(3x³+7x²)+(5x+1) ?

Jerzy: Podziel ten wielomian przez x + 1

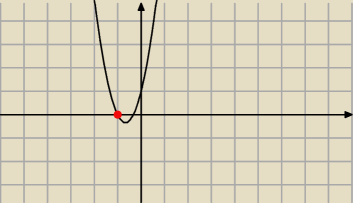
Mila: a)

	3x3+7x2+5x+1
f(x)=		dla x≠−1
	x+1

	3x3+7x2+5x+1
limx→(−1)		=
	x+1

	(x+1)2*(3x+1)
=limx→(−1)		=
	x+1

=lim_x→(−1)[(x+1)*(3x+1)=0 f(x)=0 dla x=−1 ⇔ f(x) jest ciągła w x=−1

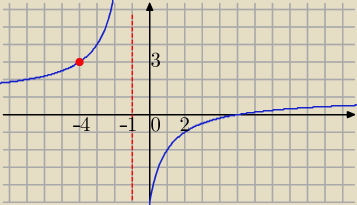
Mila: b)

	x2 −x−20		(x+4)*(x−5)		x−5
f(x)=		=		=		dla x≠(−4)
	x2+5x+4		(x+4)*(x+1)		x+1

	x2 −x−20
limx→(−4)		=
	x2+5x+4

	x−5		−4−5
=limx→(−4)		=		=3
	x+1		−4+1

f(−4)=3⇔ f(x) jest ciągła w x=−4

kajka: Dziękuję

kajka: A jak to podzieliłaś że ci wyszło (x+1)² (3x+1)

Jerzy: Nie potrafisz podzielić wielomianu przez dwumian : x + 1 ?

Mila: W(x)=3x³+7x²+5x+1 W(−1)=−3+7−5+1=0⇔x=−1 jest pierwiastkiem wielomianu Schemat Hornera: x=−1 3 7 5 1 3 4 1 0⇔3x³+7x²+5x+1=(x+1)*(3x²+4x+1) Δ=16−12=4

	−4−2		−4+2
x=		lub x=
	6		6

	1
x=−1 lub x=−
	3

	1
⇔3x3+7x2+5x+1=(x+1)*3*(x+1)*(x+		)=(x+1)2*(3x+1)
	3

Mariusz: *rozłożyć wielomian , rozwiązać równanie

szymek: nie ma funkcji odwrotnej w liceum

Mariusz: Jak ja chodziłem to jeszcze była W takim razie może być problem z obliczeniem kąta dla tzw casus irreducibilis Gdybyśmy mieli funkcję odwrotną to zdefiniowalibyśmy sobie funkcję odwrotną do cosinusa bądź sinusa która liczyłaby nam kąt

Mariusz: szymek zgadnij dlaczego udało mi się przedstawić metodę rozwiązywania równań wielomianowych Vaxowi ?

szymek: kkktórą metodę?

jc: Mariusz, sądzę, że nie o to w szkole chodzi. Przy okazji, tylko raz widziałem sensowne zastosowanie wzorów Cardano. Rzecz dotyczyła funkcji tworzących, a wiec czegoś, co lubisz. Znaczenie wzorów Cardano było podobne do znaczenia WTF. Dla matematyki nieistotne, ale doprowadziły do stworzenia ważnych narzędzi i teorii.

Mariusz: szymek chodziło mi o to że pisaliśmy głównie na gg Na forum na którym pisaliśmy była też możliwość pisania na prywatne wiadomości ale korzystaliśmy z tego tylko do pewnego momentu Do rozwiązania równania czwartego stopnia potrzebne jest rozwiązania równania trzeciego stopnia

jc: Mariusz, masz rację, to jest nawet ładne, ale to nie jest teraz ważne.

Mariusz: Ja tyko zwóciłem uwagę na to że sposób pokazany przez Mila nie jest ogólny tzn dotyczy tylko pierwiastków wymiernych oraz na to że można pokazać licealiście metodę dla tych równań a ty wyskoczyłeś z tą bezczelnością Wprawdzie dostałem się na nauczycielskie studia fizyki i matematyki ale ich nie skończyłem więc nie miałem dydaktyki Gdybym skończył to bym wiedział jak uczyć a tak to trochę intuicyjnie podchodzę do tematu Nie jest aż tak źle jak pisałeś bo jednak pokazałem Vaxowi jak rozwiązywać równania trzeciego i czwartego stopnia Zefowi też bym pokazał jak całkować gdyby tylko chciał trochę algebry liniowej ze mną poćwiczyć bo z granicami i pochodnymi jakoś sobie radzi Jeśli chodzi o zefa to przypominam że on sam chciał całkować ale jednak może lepiej żeby zajął się tematami które podała Mila

Iryt: Zasady nauczania https://womgorz.edu.pl/files/File/Pracownia_Metodyczna/Zasady_dydaktyczne[1]_1.pdf

Mariusz: 3x³+7x²+5x+1=0

	7
x=y−
	9

	7		7		7
3(y−		)3+7(y−		)2+5(y−		)+1=0
	9		9		9

	7		49		343		14		49		35
3(y3−		y2+		y−		)+7(y2−		y+		)+5y−		+1=0
	3		27		729		9		81		9

	49		1029		98		343		35
3y3−7y2+		y−		+7y2−		y+		+5y−		+1=0
	9		729		9		81		9

	4		−1029+3087−2835+729
y3−		y+		=0
	27		3*729

	4		16
y3−		y−		=0
	27		729

y=u+v

	4		16
(u+v)3−		(u+v)−		=0
	27		729

	4		16
u3+3u2v+3uv2+v3−		(u+v)−		=0
	27		729

	16		4
u3+v3−		+3(u+v)(uv−		)=0
	729		81

	16
u3+v3−		=0
	729

	4
3(u+v)(uv−		)=0
	81

	16
u3+v3=
	729

	4
uv=
	81

	16
u3+v3=
	729

	64
u3v3=
	531441

	16		64
t2−		t+		=0
	729		531441

	8
(t−		)2=0
	729

	8
u3=
	729

	8
v3=
	729

	2		2		4
y=u+v=		+		=
	9		9		9

	4		7		1
x=		−		=−
	9		9		3

x²+2x+1 3x³+7x²+5x+1:(3x+1) 3x³+x² 6x²+5x+1 6x²+2x 3x+1 0 ( x²+2x+1)(3x+1)=0 (x+1)²(3x+1)=0 NWD wielomianów też tutaj by zadziałało bo pozwala usunąć pierwiastki wielokrotne jc przeliczyłeś że wiedziałeś że ładnie wychodzi czy wywnioskowałeś to na podstawie rozwiązania użytkownika Mila bądź ze współczynników tego wielomianu

RJS: Mariusz a ze mną nie chciałbyś poćwiczyć całek, znam algebrę, ale chodzi mi bardziej o całki trygonometryczne, krzywoliniowe i powierzchniowe