Udowodnij ......(zespolone ) 6latek: Zadanie nr 726 . Udowodnij zwiazki a) |z^*|=|z| b) Argz^*=−Argz c) z*z^*=|z|² d) z+z^*∊R e) z−z^* jest liczba urojona a) z=x+iy z^*= x−iy |z|=√x²+y² |z^*|= √x²+(−y)²= √x²+y² czyli |z|=|z^*| c) (x+iy)(x−iy)= x²−i²y²= x²+y²=(√x²+y²)²= |z|² d) z+z^*= x+iy+x−iy=2x a x jest liczba rzczywista e) z−z^*= x+iy−(x−iy) = 2iy a to jest czesc urojona liczby zespolonej natomiast jesli chodzi o b to wedlug mnie bedzie tak

	−y
z*=x−iy to tgφ=
	x

	y
z=x+iy to tgφ=
	x

czyli Argz^*=−Argz Zadanie 727 Udowodnij zwiazki a) −−−−−−−−−−−−=z₁^*±z₂^* z₁±z₂ b)−−−−−−−−−=z₁^* *z₂^* z₁*z₂

	z1*
c) −−−−−−−− =		)
	z2*

	z1
(		)
	z2

d) −−−− =(z^*)ⁿ a b c potrafie udowodnic tylko tutaj nie potrafie tego zapisac dobrze natoniast w d) mam skorzystac z Tw Moivera (zⁿ) Zadanie nr 728 Na podstzwie zadan 726 i 727 uzupelnuj twierdzenie Jesli liczba zespolona z₀ jest pierwiastkiem wielomianu W(z) o wspolczynnikach rzeczywistych to liczba .... ..... ..... ..... jest tez pierwiastkiem tego wielomianu b) Udowodnij to twierdzenie

6latek: To zadanie 728 a) ja mysle ze na podstawie wvzorajszych zadan gdzie korzystalem z ewzorow Vieta to w miejsce kroppek nalezaby wpisac zepolona z nia sprzezona jest tez pierwiastkiem tego wielomianu Udowodnic tego nie potrafie (nie lubie w ogole dowodow )

Benny: Cześć małolacie W(z)=a_nzⁿ+...+a₁z+a₀ W(z*)=a_n(z*)ⁿ+...+a₁z*+a₀ ale współczynniki są rzeczywiste to wiemy, że a_i=a_i*, więc W(z*)=(W(z))* W(z)=(z−z₀)Q(z) W(z*)=(z*−z₀)Q(z*) (W(z*))*=W(z) W(z)=[(z*−z₀)*]Q(z) W(z)=(z−z₀*)Q(z) Nie wiem czy zrozumiale to napisałem. Jak coś to pytaj.

6latek: Czesc Na razie dzieki . Pozniej dopytam

6latek: Dobrze W(z) i w(z^*) to rozumiem Wiemy ze wspolczynniki a_i i a_i^* sa rzeczywiste no bo liczba zespolona i sprzezona rozni sie tylko czescia urojona Teraz tak napisales ze W(z^*)= (W(z))^* Z ktorej wlasnosci skorzystales? Najpierw to jesli mozesz

Saizou : Łatwo to pokazać np. z postaci wykładniczej liczby zespolonej

Saizou : idea jest taka że piszesz ten wielomian potem grupujesz na część rzeczywistą i urojoną i praktycznie masz koniec

Benny: W(z)=a_nzⁿ+...+a₁z+a₀ W(z*)=a_n(z*)ⁿ+...+a₁z*+a₀ wiemy, że a_i=a_i*, więc W(z*)=(a_n*)(z*)ⁿ+...+(a₁*)z*+a₀* wiemy też, że (a*)*b*=(ab)* W(z*)=(a_nzⁿ)*+...+(a₁z)*+a₀* suma sprzężeń to sprzężenie sumy, więc W(z*)=(a_nzⁿ+...+a₁z+a₀)*=(W(z))*

jc: Załóżmy, że a_i ∊ R. Wtedy (a₀ + a₁ z + ... + a_nzⁿ)^* = a₀^* + (a₁z)^* + ... + (a_nzⁿ)* = a₀^* + a₁^*z^* + ... + a_n^*(z^*)ⁿ = a₀ + a₁ z^* + ... + a_n (z^*)ⁿ Druga równość − sprzężenie sumy = suma sprzężeń. Trzecia równość − przężenie lioczynu = iloczyn sprzężeń. Ostatnia równośc: założenie, że współczynniki są rzeczywiste. Czyli w przypadku naszego wielomoanu W(z)^* = W(z^*). Jeśli więc W(z) = 0, to W(z^*)=0.

jc: Inna numeracja równań, zmieniłem tekst, a komentarz pozostał. To samo napisał Benny.

6latek: WitajSaizou Postac wykladnicza na razie nie . W sumie to dla mnie jest wazne mysle zeby wiedziec ze takie jest twierdzenie (tak mysle ) jesli chodzi o dowod to moze sie przyda jakiemus studentowi . Dobrze jest poznac jesli sie rozumie , a jesli nie to tez dobrze Mam jeszcze zadanie w tym zbiorze na temat relacji w liczbach zespolonych ale to dla mnie juz za trudne i nie bede go wstawial Jesli chcesz to go napisze .

6latek: Witaj jc Spojrz na moje zadanie z postaci trygonometrycznej jesli mozesz Dzieki za pokaznie dowodu

jc: [ r (cos α + i sin α) ]^* = r (cos α − i sin α) = r (cos (−α) + i sin (−α) ) Nie używaj argumentu głównego. Ile to jest Arg (−1) ?

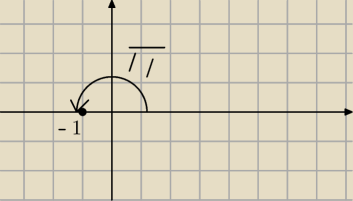
6latek: Arg(−1)=π

6latek: Dobranocjc Wroce do tego juz jutro gdyz rano do pracy

jc: W takim razie π = Arg (−1) = Arg (−1)^* = − Arg (−1) = − π i mamy problem. Lepiej nie używać argumentu głównego.

Mila: Sprzężenie liczby rzeczywistej (liczby zespolonej o zerowej części urojonej) jest równe tej liczbie.

jc: Mila, druga równość wynika ze wspomnianego przez Ciebie faktu. Chodzi o problemy z używaniem argumntu głównego. W zadaniu było Arg z^* = − Arg z. Myślę, że w algebrze lepiej nie używać argumetu głównego, tylko utożsamiać kąty różniące się o 2π. Jeśli bardzo chcemy, możemy używać argumentu głównego, ale jest to kłopotliwe (zamiast zwykłych działać należy wykonywać działania modulo 2π).

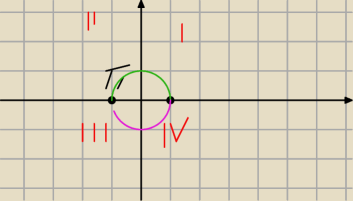
6latek: Dzien dobry Milu Dzisiaj wlasnie minelo pol roku kiedy odeszla ode mnie mam do tego watku pytanie Otoz jestem troche skolowany gdyz gdzie nie spojrze licza w przedziale 0≤φ<2π jc piszse zeby przyjmowac przedzial <−π,π> (tak to zrozumialem Wobec tego skoro mam przyjmowac ten przedzial to liczby zespolone w 1 i 2 cwiartce beda mialy argument dodatni i n

	3		3
z=−1+i zapiszsemy z=1(cos		π+isin		π)
	4		4

=========================================== Natomiast liczby zespolone w 3 i 4 cwiatce beda mialy argument ujemny

	5
np z=−1−i tgφ=1 φ=225o =		π
	4

	5		3
Teraz		π−2π= −		π
	4		4

Wobec tego

	3		3
z=−1−i to z=1(cos(−		)π+isin(−		π)
	4		4

================================== I to zostawic w takiej postaci? A jak taka postac bedzie wygladac do pierwiastkowania lub do potegowania ?

jc: Dzień dobry 6latku Ja radzę w ogóle nie przejmować się przedziałem, czyli posługiwać się zwykłym argumentem, a nie głównym.

6latek: dzien dobry Jestem troche zdezoreintowany gdyz np z= 4−i

	1
Obraz w 4 cwiartce wiec tgφ=−		z tablic odczytuje ze φ=14o2'
	4

z=√17(cos(−14^o2')+isin(−14^o2') i taka tez mam odpowiedz Natomiast z=−1−2i Obraz w 3 cwairtce wiec tg φ=2 tgφ=2 to φ=63^o30' Liczymy dalej 180^o+63,30'=243^o,30' teraz 243^o'26'−360^o= −116^o30' wobec tego z=√5(cos(−116^o,30')+isin(−116^o,30') Natomiast w odpowiedzi mam tak z=√5(cos243^o,26'+isin(243,26') Chyba nie wzialem lepszsej poprawki (mniejsza z tym Teraz nie wiem bo raz przyjmuje przedzial taki a raz inny czy lepiej obrac przedzial 0≤φ<2π?

jc: Powtórzę, nie przejmuj się takimi drobiazgami. −116 to kąt tak samo dobry, jak kąt 244. Takie rozróżnienie ma sens, jak wchodzisz na wieżę po kręconych schodach.

6latek: Dobrze czyli mamy to wyjasnione