Moduly liczb zespolonych
6latek: Zadanie 714
a) Na podstawie interetacji geometrycznej |z| uzasadnij nierownosci
||z
1|−|z
2||≤|z
1+z
2|≤|z
1|+|z
2|
b) Dla jakich a
1 i z
2 zachodza rownosci
|z
1+z
2|=|z
1|+|z
2|
|z
1−z
2|= |z
1|−|z
2|
c) Dla jakich z
1 i z
2 zachodzi rownosc
|z
1+z
2|
2= |z−1|
2+|z
2|
2
d) Dla jkaich z
1 i z
2 zachodzi rownosc
| | 1 | |
Arg(z1+z2)= |
| (Argz1+Arg z2) |
| | 2 | |
e) Dla jakich z
1 i z
2 zachodzi rownosc
Arg(z
1+z
2)= Arg(z−1)
f) Udowodnij wzor
|z
1+z
2|
2+|z−1−z
2|
2= 2(|z
1|
2+|z
2|
2)
Podaj interpretacje geometryczna tego wzoru
Wiem ze |z| to bedzie wektor
Troche przydlugie to zadanie no ale takie bylo w zbiorku
16 lip 20:31
6latek: w c) =|z1|2+|z2|2
16 lip 20:38
Saizou :
f)
niech z1=a+bi , z2=c+di wówczas
|z1+z2|2=|a+c+i(b+d)|2=(a+c)2+(b+d)2 analogicznie mamy
|z1−z2|2=(a−c)2+(b−d)2 stąd
|z1+z2|2+|z1−z2|2=(a+c)2+(b+d)2+(a−c)2+(b−d)2=
a2+2ac+c2+b2+2bd+d2+a2−2ac+c2+b2−2bd+d2=
2a2+2c2+2b2+2d2=
2(a2+b2+c2+d2)=2(|z1|2+|z2|2)
16 lip 20:48
6latek: Czesc

dzieki
A interpretacja geometryczna to bedzie przesuniecie czy obrot ?
16 lip 20:53
Saizou :
c)
niech z1=a+bi , z2=c+di wówczas
|z1+z2|2=(a+c)2+(b+d)2
|z1|2+|z2|2=a2+b2+c2+d2 stąd
a2+2ac+c2+b2+2bd+d2=a2+b2+c2+d2
ac=−bd
(zastanów się kiedy to ma rozwiązanie)
16 lip 20:54
6latek: Wtedy kiedy |z1|=−|z2|
16 lip 20:59
6latek: Chyba jednak nie
wtedy gdy z
1=−z
2
Chociaz akuratnie jest odpowiedz do tego podpunktu i pisze tak
16 lip 21:04
Saizou :
a w f) jest to przesunięcie, ale mogę się mylić

nie lubię algebry

16 lip 21:47
Metis: Siemka
Saizou
Jak tam Ci leci ?

16 lip 21:48
6latek: DObrze .
A potrafisz wytlumaczyc a?
To najbardziej mnie interesuje
16 lip 21:50
Mila:
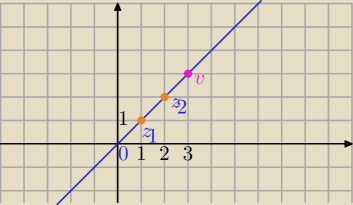
Komentarz do (b)
Dla dowolnych liczb zespolonych z
1, z
2 zachodzi nierówność:
|z
1+z
2|≤|z
1|+|z
2|
jest ona równością jedynie wtedy, gdy punkty płaszczyzny odpowiadające liczbom:
0,z
1,z
2 leżą na jednej prostej przy czym 0 nie leży między z
1, z
2.
Prosty przykład:
v=z
1+z
2
z
1=1+i
z
2=2+2i
v=3+3i
|z
1+z
2|=|3+3i|=
√18=3
√2
|z
1|=
√2
|z
2|=2
√2
−−−−−−−−−−−−−−−−−
Jeżeli punkty 0, z
1,z
2 inaczej są ułożone to masz zwykłą nierówność trójkąta.
16 lip 22:00
ICSP: Jedno małe sprostowanie:
|z| nie jest wektorem.
16 lip 22:07
Saizou :
tutaj masz zwięzły pdf o własnościach, str. 5 to co cie interesuje
http://www.fuw.edu.pl/~urbanski/Alg_I.pdf
Metis a u mnie jakoś leci, mam poprawkę we wrześniu z jednego przedmiotu,
ale mimo to średnia coś koło 4,3. Uwzględniając to że poprawię na 3.
A u Ciebie jak ?
16 lip 22:09
6latek: Dobry wieczor
Milu 
Czesc
ICSP 
Juz doczytalem |z| to jest dlugosc wektora
16 lip 22:13
Mila:
Saizou, z czego masz poprawkę?
16 lip 22:21
Mila:
Właśnie zapomniałam napisać o tym |z|, dobrze, że
ICSP czuwa.

16 lip 22:24
Saizou :
Paradoksalnie nie z przedmiotu matematycznego, tylko informatycznego,
tzn. z podstaw programowania
16 lip 22:24
Metis: Do września masz jeszcze sporo czasu, to sobie nadrobisz wszystko pewnie.
Dasz radę

Ja dzisiaj wróciłem z Wrocławia i szukam lokum

Początki

16 lip 22:26
Saizou :
To powodzenia, na pewno coś znajdziesz

16 lip 22:32
jc: W punkcie (f) masz tożsamość równoległoboku
|z+w|2 + |z−w|2 = 2 |z|2 + 2 |w|2
suma kwadratów przekątnych = podwojona suma kwadratów boków
16 lip 22:52
6latek: Czesc
jc 
Bo |z+w| to dodawanie liczb zespolonych i iterpretacja geometyczna to dluzsza przekatna
rownolegloboku
|z−w| interpretacja geometryczna jest krotsza przekatna rownolegloboku
16 lip 22:59
Mila:
Saizou, Posiedzisz przy komputerze i będzie zaliczone.
Dobrze, że matematykę masz zdaną.
16 lip 23:02
jc: Czasem dłuższa, czasem krótsza

16 lip 23:03
 dzieki
A interpretacja geometryczna to bedzie przesuniecie czy obrot ?
dzieki
A interpretacja geometryczna to bedzie przesuniecie czy obrot ?
 nie lubię algebry
nie lubię algebry 

 Komentarz do (b)
Dla dowolnych liczb zespolonych z1, z2 zachodzi nierówność:
|z1+z2|≤|z1|+|z2|
jest ona równością jedynie wtedy, gdy punkty płaszczyzny odpowiadające liczbom:
0,z1,z2 leżą na jednej prostej przy czym 0 nie leży między z1, z2.
Prosty przykład:
v=z1+z2
z1=1+i
z2=2+2i
v=3+3i
|z1+z2|=|3+3i|=√18=3√2
|z1|=√2
|z2|=2√2
−−−−−−−−−−−−−−−−−
Jeżeli punkty 0, z1,z2 inaczej są ułożone to masz zwykłą nierówność trójkąta.
Komentarz do (b)
Dla dowolnych liczb zespolonych z1, z2 zachodzi nierówność:
|z1+z2|≤|z1|+|z2|
jest ona równością jedynie wtedy, gdy punkty płaszczyzny odpowiadające liczbom:
0,z1,z2 leżą na jednej prostej przy czym 0 nie leży między z1, z2.
Prosty przykład:
v=z1+z2
z1=1+i
z2=2+2i
v=3+3i
|z1+z2|=|3+3i|=√18=3√2
|z1|=√2
|z2|=2√2
−−−−−−−−−−−−−−−−−
Jeżeli punkty 0, z1,z2 inaczej są ułożone to masz zwykłą nierówność trójkąta.
 CzescICSP
CzescICSP  Juz doczytalem |z| to jest dlugosc wektora
Juz doczytalem |z| to jest dlugosc wektora

 Ja dzisiaj wróciłem z Wrocławia i szukam lokum
Ja dzisiaj wróciłem z Wrocławia i szukam lokum  Początki
Początki 

 Bo |z+w| to dodawanie liczb zespolonych i iterpretacja geometyczna to dluzsza przekatna
rownolegloboku
|z−w| interpretacja geometryczna jest krotsza przekatna rownolegloboku
Bo |z+w| to dodawanie liczb zespolonych i iterpretacja geometyczna to dluzsza przekatna
rownolegloboku
|z−w| interpretacja geometryczna jest krotsza przekatna rownolegloboku
