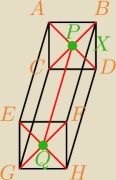
Wierzchołki prostopadłościanu supra: Tworzę aplikację z grafiką 3D na androida na swoją pracę inżynierską, i muszę znaleźć wzory na znalezienie pewnych wartości. Jak widać na rysunku mam pewne dane (zielony) i szukane (pomarańczowy) DANE: P (x1,y1,z1) Q (x2,y2,z2) X − długość boku przekroju SZUKANE: A (ax,ay,az) B (bx,by,bz) C (cx,cy,cz) D (dx,dy,dz) E (ex,ey,ez) F (fx,fy,fz) G (gx,gy,gz) H (hx,hy,hz) Mam nadzieje że w ogóle jest możliwość uzyskania takich wzorów aby uzyskać z tych trzech danych, wierzchołki prostopadłościanu Z góry dzięki za każde zainteresowanie się próbą utworzenia tych wzorów

jc: Końce osi nie wystarczą. Bryła może się obracać względem osi. Przydałaby się jeszcze jakaś informacja.

supra: jeszcze mogę dodać kąt obrotu względem długości QP

jc: Jeśli byś miał jakikolwiek wektor nierównoległy do u=P−Q, to byłoby prosto. Oznaczmy taki wektor literą v. Wektor w = v − (u*v)/(u*u) u jest prostopadły do u. * oznacza iloczyn skalarny. n = w / |w| = unormowany wektror prostopadły do u. k = |u|⁻¹ n x u = unormowany wektor prostopadly do u i n. x 0znacza iloczyn wektorowy. A − P = X/√2 n tzn. A = P + X/√2 n B − P = X/√2 k tzn. B = P + X/√2 k Pozostałe punkty znajdziesz łatwo z równości: P − Q = A − E = B − F = C − G = D − H

supra: "w = v − (u*v)/(u*u) u" czy to miało być w = v − (u*v)/(u*u)(razy)u ? w sensie czy wektor "u" ma być pomnożony przez stałą wychodzącą z: (u*v)/(u*u) ?

jc: A jak inczej? Można też przyjąć w = (u*u) v − (u*v) u. Może nawet lepiej. Potem i tak normujemy w

supra: analogicznie do równań A i B napisałem do pozostałych, czy są dobre ? C + P = X/√2 n D + P = X/√2 k E − Q = X/√2 n F − Q = X/√2 k G + Q = X/√2 n H + Q = X/√2 k

jc: Raczej tak: A = P + X/√2 n B = P + X/√2 k C = P − X/√2 n D = P − X/√2 k E = Q + X/√2 n F = Q + X/√2 k G = Q − X/√2 n H = Q − X/√2 k

supra: hmm niestety nie działa tak jak powinno, a więc mam pytanie, czy ten wektor "v" może być np. wektorem "u" w którym zmienię jedną wartość ?

jc: Nie wiem, co nie działa. Jaki efekt chcesz uzyskać? Poniżej kod w Pythonie, który działa. ux, uy, uz = 1.0, 2.0, 3.0 vx, vy, vz = 2.0, 5.0, 2.0 u = (ux*ux + uy*uy + uz*uz)**0.5 ux, uy, uz = ux/u, uy/u, uz/u uv = ux*vx + uy*vy + uz*vz nx, ny, nz = vx−uv*ux, vy−uv*uy, vz−uv*uz n = (nx*nx+ny*ny+nz*nz)**0.5 nx, ny, nz = nx/n, ny/n, nz/n kx, ky, kz=ny*uz−nz*uy, nz*ux−nx*uz, nx*uy−ny*ux Gdybys kopiował, to popraw minusy na prawdziwe! Możesz też tak zakończyć A = P + (X/2)(n+k) B = P + (X/2)(n −k) C = P + (X/2)(−n+k) D = P + (X/2)(−n−k) Czy jakoś podobnie.

supra: w androidzie muszę zadeklarować każdą funkcję związaną z dodawaniem odejmowaniem mnożeniem i dzieleniem wektorów więc mam trochę inaczej public static float[] ConnectionModule(float startX, float startY, float startZ, float endX, float endY, float endZ, float x) { float[] u = { // wektor tych twóch punktów endX − startX, endY − startY, endZ − startZ }; float[] v = { // wektor nie równoległy do "u" endX − startX + 1, endY − startY, endZ − startZ }; float uov = u[0] * v[0] + u[1] * v[1] + u[2] * v[2]; // iloczyn skalarny "UoV" float uou = u[0] * u[0] + u[1] * u[1] + u[2] * u[2]; // iloczyn skalarny "UoU" float[] w = { // wektor prostopdły do "u" v[0]*uou − u[0]*uov, v[1]*uou − u[1]*uov, v[2]*uou − u[2]*uov }; float moduloW = (float) Math.sqrt(w[0] * w[0] + w[1] * w[1] + w[2] * w[2]); // długość wekrota w float[] n = { // unormowany wektor prostopadły do "u" w[0] * 1 / moduloW, w[1] * 1 / moduloW, w[2] * 1 / moduloW }; float moduloU = (float) Math.sqrt(u[0] * u[0] + u[1] * u[1] + u[2] * u[2]); // długość wektora u float[] k = {// unormowany wektor prostopadły do u i n 1 / moduloU * (n[1] * u[2] − n[2] * u[1]), 1 / moduloU * (n[0] * u[2] − n[2] * u[0]), 1 / moduloU * (n[0] * u[1] − n[1] * u[0]) }; to jest ten początek może coś źle zrozumiałem

Dziadek Mróz: Napisz sobie klasę Vector3 dla punktu 3d i nie śmieć sobie kodu

jc: To jest strasznie napisane ... Chcesz operować na wektorach, zdefiniuj wektory, dodawanie wektorów, mnożenie przez skalar, iloczyn skalarny, iloczyn wektorowy. Ale może trzeba zupełnie inaczej spojrzeć na problem. Co chcesz uzyskać? Co ma robić program?

supra: cały program ma liczyć kinematykę prostą i odwrotną manipulatora (robota) o szeregowej i dowolnej konfiguracji, ale to co teraz się pytam jest mi potrzebne do wyświetlania wyniku tego co zadeklaruje użytkownik, w sensie po obliczeniu wszystkich współrzędnych muszę połączyć dwa ogniwa, najlepiej by było w tym przypadku jakimś walcem, ale niestety w androidzie mogę tylko zadeklarować punkty które później będą połączone w płaszczyzny. Wiem że jest trochę zaśmiecone ale najpierw chcę żeby to zadziałało a potem będę to poprawiać żeby to lepiej wyglądało

jc: Czyli belka to element manipulatora. Czy kąt pod jakim przekręcona jest belka wynika z konstrukcji manipulatora, czy jest dowolny? Czy ładniej wyglądałby walec, czy belka? Walec będzie prostokątem zakończonym łukami elipsy. Myślę, że to da się ładnie narysować. Na koniec z ciekawości spytam, czy wynik chcesz prezentować w rzucie perspektywicznym, czy prostokątnym?

jc: Spytam inaczej, czy odcinek AB jest poziomy? a jesli nie, to od czego zależy jego nachylenie.

supra: Jak zrobiłem ten kod co wysłałem to wyszła mi płaszczyzna a nie prostopadłościan dla tego się zastanawiałem czy nie mam błędu w obliczeniach. W moim przypadku obrót belki nie wynika z konstrukcji manipulatora. Tak, lepiej było by z walcem, ale android przyjmuje punkty które łączy w odpowiedniej kolejności więc nie mogę zadeklarować np. łuku. Będę to pokazywać w rzucie perspektywicznym. Nachylenie jest dowolne.

supra: poprawiłem przejrzystość kodu: public static float[] ConnectionModule(float[] start, float[] end, float x) { float[] u = ActionMatrix.Subtraction(end, start); float[] v = { u[0] + 1, u[1], u[2] }; float[] w = ActionMatrix.Subtraction(v, ActionMatrix.Multiplication(u, ActionMatrix.ScalarMultiplication(u, v) / ActionMatrix.ScalarMultiplication(u, u))); float[] n = ActionMatrix.Multiplication(w, ActionMatrix.Length(w)); float[] k = ActionMatrix.Multiplication(ActionMatrix.VectorMultiplication(n, u), 1 / ActionMatrix.Length(u)); }

jc: Czy możemy założyć, że odcinek AB jest poziomy? czy w trakcie ruchu obraca się. Widziałem takie manipulatory: ramię do góry, zawias, ramię do dołu, oracający się uwchwyt. Wtedy całe załamane ramię leży w płaszczyźnie pionowej. Jak jest u Ciebie? A co do grafiki w Androidzie, pewnie nie różni się od grafiki w jawie.

supra: w teorii tak jest że się obraca, ale ja tylko wyświetlam dane ramię a nim nie poruszam, więc możemy założyć że odcinek AB jest poziomy

supra: jest zupełnie inna niż a javie

jc: Chodzi o estetykę i realistyczność obrazka. Jeśli chcesz mieć poziomy odcinek AB, to przyjmij v=(1,0,0). A potem A = P + (X/2)(n+k) B = P + (X/2)(−n+k) C = P + (X/2)(n−k) D = P + (X/2)(−n−k) itd.

supra: wpadłem teraz na pewien pomysł, ponieważ pamiętam z liceum że można wyznaczyć płaszczyznę prostopadłą do wektora i przechodzącą przez punkt, i to by nie było trudne, ale teraz dało by radę wyznaczyć wzór okręgu położonym na tej płaszczyźnie którego środek by był w jakimś punkcie ?

jc: Okrąg możesz opisać jako przecięcie sfery z płaszczyzną lub parametrycznie.

supra: czyli będę miał układ równań: A(x− x₀ ) + B(y − y₀ ) + C(z− z₀) = 0 (x−x₀)² + (y−y₀)² + (z−z₀)² = r² z czego wiadome to: A,B,C, x₀, y₀, z₀ i r żeby wyznaczyć chociaż jeden punkt to potrzebne jest jeszcze jedno równanie, jest jeszcze jakieś równanie które mogło by połączyć sferę i płaszczyznę?

jc: Wzory, które napisałem o 17:38 są poprawne. Sprawdzałem wyniki numeryczne (zawsze warto sprawdzić, błąd może polegać na zamienie jednej litery na inną, a nawet słowa, w przypadku, kiedy tekst tworzy się metodą ctr−c, ctr−v).

jc: Jak masz zdefiniowany iloczyn wektorowy, to prościej będzie tak: u = (P−Q) v = (0,0,1) (nie zadziała dla pionowego ustawienia belki) n = u x v / |u x v| k = u x n / |u x n| A = P + (X/2)(n+k) B = P + (X/2)(−n+k) itd.

supra: wyświetliłem sobie punkty które powstały i wpisałem je do programu AutoCAD no i powiem że niestety wychodzi płaszczyzna, sprawdź u siebie, takie wektory ux, uy, uz = 2.0, 2.0, 2.0 vx, vy, vz = 3.0, 2.0, 2.0 i z tego powstały mi takie punkty: 3.4082484, 3.1494296, 3.1494296 3.4082484, 2.4423227, 2.4423227 2.5917516, 3.5576773, 3.5576773 2.5917516, 2.8505704, 2.8505704 1.4082485, 1.1494294, 1.1494294 1.4082485, 0.4423226, 0.4423226 0.59175146, 1.5576774, 1.5576774 0.59175146, 0.85057056, 0.85057056 i powiedz czy wyszły takie u Ciebie, będę wiedzieć czy ja mam coś źle w obliczeniach.

jc: Ja liczyłem tylko u, n, k: 0.57735026919 0.57735026919 0.57735026919 0.816496580928 −0.408248290464 −0.408248290464 0.0 −0.707106781187 0.707106781187 czyli 1/√3, 1/√3, 1/√3 unormowana os belki √2/3, −1/√6, −1/√6 wektor ⊥ os 0 −1/√2, 1/√2 wektor ⊥ do os i dwoch wczesniejszych

jc: Zwróć uwagę, że u = (P−Q) / |P−Q|

supra: mam identycznie i z wykorzystaniem tego powstaje płaszczyzna z dalszych obliczeń

supra: k mam inne, 0.0 0.707106781187 0.707106781187

supra: dobra teraz jest dobrze, dzięki wielkie , źle miałem k. To mam pytanie do takiej kwestii teoretycznej, co robi unormowanie wektorów ?

jc: Wektor unormowany, to wektor o długości jeden. Jeśli mamy wektor o długości 5, a chcemy mieć wektor o długości 7, to dzilimy wektor przez 5 (normujemy), a potem mnozymy przez 7. Oczywiście możemy od razu pomnożyć przez 7/5.

supra: czyli w tym przypadku unormowanie uproszcza dalsza obliczenia ?

supra: chyba rozumiem, jeżeli będzie większa długość wektora to ten element będzie parokrotnie większe ?