Argument glowny 6latek: Pytanie Czy mozna przyjac inne ograniczenie na wspolrzedna φ np −π<φ≤π? Czy to sie stosuje ?

6latek: Pytam dlatego ze w 2 ksiazkach pisze ze 0<φ≤2π Natomiast w jednej piszse ze bedzie sie autor staral uzywac wlasnie argumentu z tego przedzialu

jc: W jakim kontkekście? W wielu sytuacjach w ogóle można nie przyjmować żadnych ograniczeń. Wystarczy na kąty patrzyć, jak na punkty na okręgu (utożsamiać liczby różniące się o 2π).

6latek: Pytam bo zaczynam czytac o postaci trygonometrycznej liczby zespolonej Na kursie tez przyjmowal 0<φ≤2π

6latek: np z=1−i obraz tej liczby lezy w 4 cwiartce plaszzyzny Gaussa

	−1
tgφ=		=−1
	1

wiec φ=315 ^o z=√2(cos315^o+isin315^o) Przyjalem 0<φ≤2π A teraz jakby przyjac −π<φ≤π tojak bedzie wygladac postac trygonometryczna ?

ICSP: √2(cos(−45^o) + isin(−45^o))

mats: cos315 zamienia się na cos(360−315)=cos45 sin315 zamienia sie na sin(360−315)=−sin45

6latek: Dziekuje Prosilbym jednak o jakies szersze wyjasnienie

Jerzy: Przyjmuje sie za arwny przedzial

Jerzy: .. za argument glowny przedzial [−π,π]

6latek: Witaj Jerzy Jak to sie przelicza ? A co np gdyby obraz liczby zepolonej lezal w 3 cwiartce ? np z=−1−i wtedy tgφ=1 Jak to sprowadzic do tego przedzialu ? jest na to jakas regula ? Nie moge nigdzie znalezc na ten temat (w swoich ksiazkach)

6latek: Zapomnialem dopisac ze wtedy φ=225^o

6latek: Kolega wyzej pisal ze zamienia sie na cos (360−225)=cos(−135)^o=cos135 sin(360−225)=sin(−135)=−sin135 Czy to sie robi tak ?

6latek: Czy ktos moze mi to dokladnie wytlumaczyc na paru przykladach ?

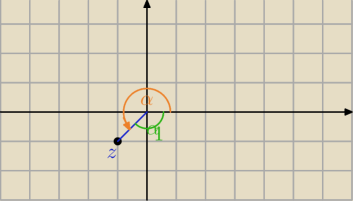
Mila: Dowolne dwa argumenty liczby zespolonej różnią się o wielokrotność 2 π . argument główny:

	5π
Arg(z)=		∊<0,2π)
	4

W obliczeniach podaje się też :

	3π		5π		3π
Arg(z)=−		∊(−π,π> [		−2π=−		]
	4		4		4

6latek: Dobry wieczor Milu To z tego wynika ze i tak musze policzyc najpierw argument z przedzialu <0,2π) i potem odjac od tego 2π Dopoki nie bede w stanie liczyc to w pamieci szybko Na razie dziekuje za wyjasnienie . Lepiej wedlug mnie bedzie przyjmowac ten 1 przedzial

Mila: Witaj Krzysiu. Jak zdrowie? Chyba dobrze, bo chodzisz do pracy.? Liczbę zespoloną zaznacz w układzie wsp. będzie łatwiej ustalić argument i niektóre argumenty od razu podasz. Ja podaję z przedziału <0,2π).

Mariusz: To jest umowne czy weźmiemy argument główny z <0,2π) czy z (−π,π>

6latek: Milu Na razie jest dobrze . Chodze do pracy teraz na 2 zmiane ,jeszcze dzisiaj . Od poniedzialku na 1 zmiane Jutro mam wolne .

6latek: czesc Mariusz Przegladajac ksiazki jednak czesciej przyjmuja przedzial <0,2π)

jc: W jakim problemie potrzebny jest argument główny? Zwykły argument na ogół jest wygodniejszy. Argument iloczynu to suma agumentów (utożsamiamy kąty różniące się o 2π). To trochę tak, jakby dopuszczać tylko ułamki nieskracalne. Można (czasem trzeba), tylko po co sobie utrudniać rachunki?

6latek: Witaj jc Moge sie zapytac tylko tutaj na forum Problem ten byl postawiony w cwiczeniu z ksiazki matematyka dla klasy 3 i 4 licem podrecznik uzupelniajacy (profil matematyczno fizyczny ) Anusiak . Jednak on jest troche wredny bo nie pokazuje np rozwiazanego przykladu tylko rzuca Cie od razu na gleboka wode . Tam w nim znalazlem temat liczb zespolonych i zaczalem go przerabiac . Mam jeszce ksiazke o tych rownaniach i tam tez sa opisane liczby zespolone a takze Eustachy Tarnawski Matematyka dla studiow technicznych

6latek: Mialem tez robic zadania z tych liczb z inne go zbioru zadan ale one sa tam trudne Wiec chyba sobie je odpuszcze tak jak te z nierownosci trojkata z modulami Zajme sie prostymi obliczeniami tj podstawowe dzialania (to umiem ) doprowadzanie do postaci trygonometrycznej , potegowanie i pierwiastkowanie liczb zespolonych mnozenie i dzielenie liczb zespolonych w postaci trygonometrycznej . To powinno mi w zupelnosci wystarczyc

Mariusz: Argument główny przydaje się gdy np z logarytmu zespolonego chcemy zrobić funkcję Jest on wtedy częścią urojoną logarytmu Zwykły argument nie pozwoliłby zdefiniować logarytmu zespolonego