obliczyć objętość bryły ograniczonej powierzczniami (całką)
lolo: y−x2=0
y−2=0
2x+y+z=4
z=1
10 lip 22:15
lolo: jak wyznacze y=2 i y=x2 to mam granice do całki podwójnej a ten z=1 co zmienia?
10 lip 22:39
Jerzy:
Masz taki kociołek jak na grilla...kręci się parabola y = x2
i obcina ją płaszczyna y = 2 , a potem wycinasz plaster od z = 1, do z równego podana funkcja
10 lip 23:15
piotr: nic tu się nie kręci
| | 24 √2 | |
∫−√2√2 ∫x22 ∫1−2 x−y+4 1 dz dy dx = |
| |
| | 5 | |
10 lip 23:28
Jerzy:
Kręci się...bo nie byłoby bryły
10 lip 23:32
piotr: mamy podane cztery równania powierzchni, to wystarczy,
lepiej treści zadania sobie nie wymyślać
10 lip 23:37
piotr:
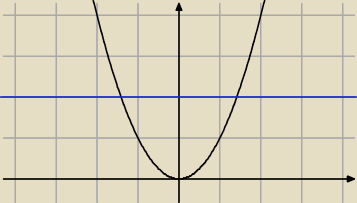
10 lip 23:39
Jerzy:
No i o tym rozmawiamy ...cztery powierzchnie ograniczają bryłę,
paraboloida y =x2 powstaje z obrotu paraboli y = x2
10 lip 23:44
piotr: nie brnij Jerzy, nie ma żadnej paraboloidy, paraboloida ma równanie np.: z= x2+y2
11 lip 00:09
Mariusz:
piotr nie wystarczyłaby całka podwójna ?
11 lip 09:42
jc: Mariusz, dziwisz się? Może było takie polecenie? Niektórzy nawet pole prostokąta znajdują
licząc całke podwójną.
11 lip 09:53
piotr1973: Podałem po prostu ogólny wzór,
przecież całka z 1 po dz chyba nie jest za trudna i po jej wykonaniu mamy całkę podwójną
11 lip 10:09
Jerzy:
To chyba mnie pokręciło

Ale całka podwójna załatwia temat

11 lip 19:03
piotr: po przeanalizowaniu całej geometrii
V=V1+V2
| | 12 √2 | | 1091 | |
V1 = ∫−√21/2 ∫x22 ∫1−2 x−y+4 1 dz dy dx = |
| + |
| |
| | 5 | | 320 | |
| | 263 | |
V2 = ∫1/21 ∫x23−2x ∫1−2 x−y+4 1 dz dy dx = |
| |
| | 960 | |
11 lip 19:18
Jerzy:
Co Ty piotr kombinujesz ?
Liczymy całkę podwójną po obszarze normalnym ograniczonym krzywymi y = x2 i y = 2
z różnicy funkcji z
11 lip 19:26
piotr: tak się jednak składa, że w obszarze normalnym ograniczonym krzywymi y = x2 i y = 2
płaszczyzna
2x+y+z=4 nie w całości znajduje się na powierzchnią z=1
11 lip 19:37
piotr: granicą jest płaszczyzna 3−2x=y (2x+y+z=4, przy z=1)
11 lip 19:39
Jerzy:
Może ja już śpię...jak coś w przestrzeni może nie leżeć pod lub nad plaszczyzną z=1
11 lip 20:29
11 lip 20:43
Jerzy:
Kuźwa...jestem w lesie na telefonie...płaszczyzna się załamuje nad obszarem ?
11 lip 20:52
jc: Jerzy, dach przecina podłogę w obrębie paraboli.
Piotrze, gratuluję poprawnego wyniku

11 lip 20:58
piotr: a skąd to zadanie?
11 lip 21:05
Jerzy:
Przekonaliście mnie

11 lip 21:13

 Ale całka podwójna załatwia temat
Ale całka podwójna załatwia temat 

