Równanie prostej Juula: Napisz równania prostej przechodzącej przez punkt (−1,0,3) i równoległej do płaszczyzny Oxz Proszę o pomoc baaardzo

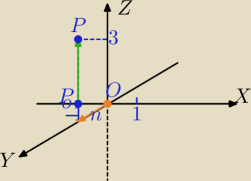
Mila: Prosta równoległa do płaszczyzny XOZ Płaszczyzna XOZ ma równanie : y=0 (x∊R, z∊R) Wektor normalny płaszczyzny XOZ: n^→=[0,1,0] P=(−1,0,3)∊prostej ale też do pł. XOZ Wybieramy drugi punkt z tej płaszczyzny np. P₀=(−1,0,0)∊szukanej prostej P₀P^→=[0,0,3] wektor kierunkowy prostej Równanie prostej: x=−1 y=0 z=3+3t, t∊R Prosta leży w płaszczyźnie XOZ.

Piotrek: Politechnika Łódzka?

Jerzy: Witaj Milu Chyba można prościej .. Skoro prosta jest równoległa do płaszczyzny OXZ, to jej wektorem kierunkowym może być np. wersor osi OZ : n^→ = [0,0,1]. Zatem szukana prosta: x = −1 + 0*t y = 0 + 0*t z = 3 + 3*t , czyli: x = −1 y = 0 z = 3 + 3t Do autora postu: jest to pęk prostych leżących w płaszczyżnie OXZ i przechodzących przez punkt P (−1,0,3)

Jerzy: No i nie ustrzegłem się błędu ( zapatrzony w Twoje rozwiązanie ) x = − 1 y = 0 z = 3 + 1*t = 3 + t

Mila: