Udowodnij (z twierdzenia Cevy) Tusia: Udowodnij, że dwie dwusieczne kątów zewnętrznych trójkąta i dwusieczna kąta wewnętrznego do nich nie przyległego przecinają się w jednym punkcie (środek okręgu dopisanego do trójkąta). Wykorzystaj twierdzenie Cevy.

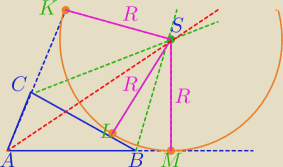
Mila: CS^→ dwusieczna kąta zewnętrznego C⇔Punkt S jest jednakowo odległy od ramion tego kąta BS^→ dwusieczna kąta zewnętrznego B⇔Punkt S jest jednakowo odległy od ramion tego kąta⇒ Punkt S jest jednakowo odległy od ramion kąta KAM ⇔leży na dwusiecznej kąta A