Dla jakich wartości k, wielomian ma 3 pierwiastki rzeczywiste Przemek: Dla jakich wartości k, wielomian ma 3 pierwiastki rzeczywiste x³−3x−k=0

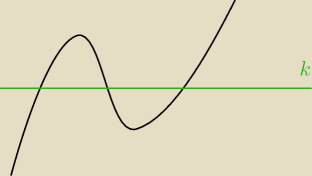
Godzio: x³ − 3x = k x(x² − 3) = k x(x − √3)(x + √3) = k f(x) = x³ − 3x f'(x) = 3x² − 3 = 3(x − 1)(x + 1) Dla x = 1 mamy minimum lokalne Dla x = −1 mamy maksimum lokalne Zatem 3 rozwiązania są gdy f(−1) > k > f(1) −1 + 3 > k > 1 − 3 2 > k > −2 k ∊ (−2,2)

jc: Trochę inaczej. Narysuj sobie dwie styczne do wykresu y = x², jedną w punkcie (−1,−1) drugą w punkcie (1,1). Styczne mają nachylenie 3. Linia y = 3x + k powinna leżeć pomiędzy stycznymi: −2 < k < 2

Metis: Równanie postaci: x³+px+q=0 ma dokładnie 3 rozwiązania, gdy jego Δ>0. Δ= −4p³−27q² p=−3 q=−k Δ=108−27k² Δ>0 ⇔ 108−27k²>0 /:27 ⇔ 4−k²>0 , stąd k∊(−2,2)

Przemek: Dzięki Godzio o to rozwiązanie mi chodziło, jc też dzięki, ciekawe podejście

Metis: Nie ma za co

Przemek: Również dzięki Metis, nie widzialem twojego wkładu jak wstawiałem posta, chociaż nie bardzo wiem skąd taka Δ

Metis: Poczytaj o równaniu sześciennym. To dość szeroko rozwinięte pojęcie w matematyce, ale nie tej szkolnej.

jc: Oczywiście miało być y =x³, nie y=x².