Geometria analityczna jakub231: Napisz rownanie okregu opisanego na trojkaιcie o wierzchołkach A = (5, −4), B = (6, −1), C = (−2, 3). Zbadaj wzajemne polozenie tego okręgu oraz jego obrazu w symetrii osiowej względem prostej 3x+4y+26=0 Chciałbym aby ktoś mi pomógł bo wychodzą mi strasznie dziwne wyniki. Więc najpierw wyznaczam środek okręgu do którego należą punkty A B C z obliczeń wychodzi że ten okrąg ma środek w punkcie P(4,2) Dalej do prostej 3x+4y+26 znajduje prostą prostopadła przechodząca przez punkt (4,2). Potem znajduje miejsce przecięcia Tych dwóch prostych przyjme że jest to punkt K. To wtedy Wektor PK jest równy wektorowi KP'. z tego wyznaczam P'(środek okręgu po przekształceniu) Znając środki okręgów tworze układ 2 równań składający się z równań okręgów o środku P i P', i dostaje odpowiedź jak on względem siebie są położone. Jeżeli mój tok rozumowania jest dobry to już przy obliczaniu punktu przecięcia się prostych prostopadły wychodzi starsznie dziwny ten punkt(−94/25,47/6)

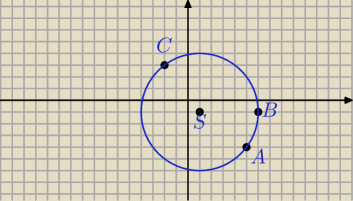
Janek191: A =( 5, −4) B = ( 6, −1) C = ( − 2, 3) (x − a)² + ( y − b)² = r² więc ( 5 − a)² + ( − 4 − b)² = r² ( 6 − a)² + ( − 1 − b)² = r² ( − 2 − a)² + ( 3 − b)² = r² 25 − 10 a + a² + 16 + 8 b + b² = r² 36 − 12 a + a² + 1 + 2 b + b² = r² 4 + 4 a + a² + 9 − 6 b + b² = r² 1) a² − 10 a + b² + 8 b + 41 = r² 2) a² −12 a + b² + 2 b + 37 = r² 3) a² + 4 a + b² − 6 b + 13 = r² 1) − 2) 2 a + 6 b + 4 = 0 / : 2 a + 3 b + 2 = 0 a = − 3 b − 2 ======= 2) − 3) − 16 a + 8 b + 24 = 0 / : 8 − 2 a + b + 3 = 0 więc −2*( − 3 b − 2) + b + 3 = 0 6 b + 4 + b + 3 = 0 7 b = − 7 b = − 1 ===== a = − 3*(−1) − 2 = 1 ============== S = ( 1 , − 1) =========

Jack: Srodek mozna tez znalezc w inny sposob, a mianownicie srodek okregu opisanego na trojkacie znajduje sie w punkcie przeciecia symetralnych jego bokow. zatem znajdzmy 2 symetralne.

malineczka : CZyli jeżeli chce odejmować stronami to np: 1)−2) a potem 2)−3), bo jak ja odejmowałem 2)−1) 2)−3) to dostałem inny wynik

Janek191: r² = 1 − 10 + 1 − 8 + 41 = 43 − 18 = 25 r = 5 === 3 x + 4 y + 26 = 0 S = ( 1 , − 1) 4 y = − 3 x − 26

	3		26
y = −		x −
	4		4

Prosta prostopadła

	4
y =		x + b
	3

	4
− 1 =		*1 + b
	3

	4
− 1 −		= b
	3

	7
b = −
	3

	4		7
y =		x −
	3		3

=============== Punkt wspólny tych prostych

	3		26		4		7
−		x −		=		x −		/ * 12
	4		4		3		3

− 9 x − 78 = 16 x − 28 25 x = − 50 x = − 2 ====

	4		7		8		7
y =		*(−2) −		= −		−		= − 5
	3		3		3		3

========================= S₁ = (− 2, − 5 ) ============== zatem

1 + x		−1 + y
	= − 2 i		= − 5
2		2

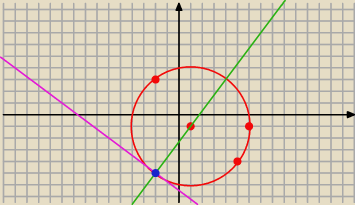
1 + x = − 4 i − 1 + y = − 10 x = − 5 i y = − 9 S ' = ( − 5, − 9 ) =========== r = 5 I S S 'I² = ( − 5 − 1)² + ( − 9 + 1)² = 36 + 64 = 100 I S S ' I = 10 = 2 r więc okręgi są styczne w punkcie S₁ = ( − 2, − 5)

Mariusz: Na podstawie danych wierzchołków długości boków Z twierdzenia cosinusów cosinusy kątów w trójkącie Z jedynki trygonometrycznej sinusy kątów Z twierdzenia sinusów długość promienia Długość promienia to odległość od środka okręgu do jednego z wierzchołków trójkąta