oblicz całkę Michalina: oblicz całkę ∭zdxdydz gdzie K zawiera punkt (0,0,−√8) oraz jest ograniczone x²+y²+z²=8, z²=x²+y² jak wyznaczyć przedziały całkowania

Leszek: co to jest K , gdzie on ma należeć ?

Michalina: K to obszar całkowania

g: Innymi słowy z²=4 oraz x²+y²=4, czyli że K to są dwa okręgi. Chyba nie tak miało być.

Michalina: co ty za głupoty piszesz. obszarem jest kula i stożek

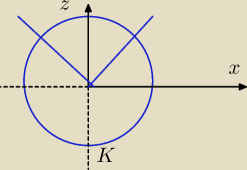
Leszek: patrząc na rysunek w płaszczyznie ZX coś się nie zgadza , bowiem wydaje się że bryłą jest stożek z czaszą

Qulka: skoro K zawiera ten punkt na dole to jest to kula z wydrążoną parabolidą

Qulka: i po prostu trzeba policzyć jej objętość

Leszek: z wydrążonym stożkiem z wieczkiem w kształcie czaszy

	4π√83
wobec tego od objętości kuli Vk=		należy odjąć objętość tej bryły
	3

w kształcie stożka V_st= ∫ ∫ dxdy[ √8−(x²+y²)−√x²+y²] D D; x²+y² =8 we współrzędnych biegunowych r ∊ <0;√8> i φ ∊ <0 ;2π >

Leszek: SORRY r ∊ <0, 2>

Qulka: http://prntscr.com/bl0zs4 zadanie 57

Michalina: tylko zwróćcie uwagę na to ze tam jest całka do policzenia a nie objętość całka to∭z dxdydz

Qulka: to do tych obliczeń w linku w pierwszej linijce pod obrazkiem 40 zamiast [z] wstaw [z²/2] i policz

jc: Kula ma promień R=2√2. Czasza zaczyna się na wysokości R/√2. Pole czaszy wynosi 2πR (R−R/√2) i stanowi 2πR² (1−1/√2)/(4πR²)= (1−1/√2)/2 część sfery. Objetość takie wycinka wynosi więc

	2−√2
V = 4/3 π R3 (1−1/√2)/2 =		π R3
	3

jc: Też dopiero teraz zauważyłem z pod całką To może lepiej od razu rozwiązać ogólniejsze zadanie: Na jakiej wysokości leży środek masy rożka o kącie rozwarcia równym α ? Rachunek podobny, a wynik z parametrem i można się cieszyć zmieniając jego wartość.

piotr: ∫₀^2π ∫₀² ∫_π/4^π r²sinφ cosφ dφ dr dθ

jc: powinno być r³ zamiast r²

piotr: poprawka: ∫₀^2π ∫₀² ∫_π/4^π r³ sinφ cosφ dφ dr dθ = −2π

jc: Ojej, autor wymysli, żeby policzyć kulę z wydrążonym stożkiem ... skąd taki pomysł. Czy całkowanie względem r nie powinno się zakończyć na √8 ?

piotr: Dzięki jc, teraz już poprawnie: ∫₀^2π ∫_π/4^π ∫₀^√8 r³ sin(φ) cos (φ) dr dφ dθ = −8π

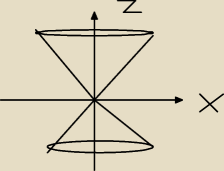
Michalina: cały czas wydaje mi się ze jest źle bo równanie x²+y²=z² opisuje stożek do góry i do dołu więc nadal myślę że rozpatrujemy stożek z sferycznym denkiem gdzie θ=(3/4π, π) φ=(0,2π) i jakieś r

Leszek: A gdzie u Ciebie jest sfera ? ,oraz z =√x²+v² to wspolrzedna (z) jest wieksz od 0

piotr: ∫₀^2π ∫₀^π/4 ∫₀^√8 r3 sin(φ) cos (φ) dr dφ dθ = 8π ∫₀^2π ∫_3π/4^π ∫₀^√8 r3 sin(φ) cos (φ) dr dφ dθ = −8π

g: Określanie obszaru K równaniami powierzchni ograniczających może prowadzić do nieporozumień. Czy nie lepiej napisać że K to obszar spełniający obie nierówności: x²+y² ≤ 4 x²+y²+z² ≤ 8

Michalina: jest sfera wyraźnie opisana tym równaniem x²+y²+z²=8 oraz stożek opisany tym z²=x²+y²

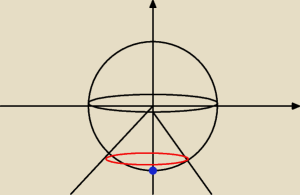
Michalina: r dużej sfery wynosi √8. Niebieski punkt to (0,0,−√8) r czerwone przecięcie sfery i stożka to x²+y²=8−x²−y² r=2 θ odczytane z rysunku to 3/4π do π całka wygląda tak ∭rcosθ r²sinθ dθdφdr gdzie granice całkowania to r(0,2) θ(3/4π, π) φ(0,2π) po przecałkowaniu wychodzi mi −4π√2 @LESZEK zwróć uwagę że z=√x²+y² oraz z=−√x²+y²

Michalina: sorry wyszło −2π

Leszek: Tresc zadania nie jest zbyt jednoznacznie napisana ,czy jest to calka ∫∫∫zdxdydz ? I do obszaru calkowania nalezy p. K Wowczas wydaje mi sie ze chodzi o objetosc bryly ,czyli kuli z wydrazonym stozkiem Ale moge sie mylic ?

jc: Tak, jak piszesz, tylko to nie jest obkętość, a moment.

Leszek: Jaki moment bezwladnosci czy statyczny ,w obu musi byc podana os ,a tego w tresci zadania nie ma. A moze chodzi o tensor momentu bezwladnosci ,ale to tylko nasze domysly,tresci zadan matematycznych powinny byc podawane precyzyjnie .

jc: ∫∫∫ z dxdydz / ∫dxdydz = z−towa składowa środka masy Jeśli weźmiemy rożek o rozwartości 2α (z dziubkiem skierowanym w dół), to środek masy znajdzie się w punkcie

	1+cos α/2		3
z =				R
	2		4

α = 2π, cała kula, z=0 α = π, półkula, z= (3/8)R

Michalina: Co wy za głupoty wypisujecie. Polecenie ejst obliczyć całkę ∫∫∫z po obszarze K ograniczonym sferą i stożkiem zawierającym punkt ww.

jc: Przecież masz już wynik: −2π. Do czego Ci ta całka potrzebna?

Leszek: Szanowna p.Michalino punkt K(0,0,−√8) nie jest obszarem ,jak punkt moze miec obszar czyli powierzchnie. Prosze nie obrazac piszacych tylko pisac poprawnie i logicznie tresci zadan,Matematyka jest nauka logiczna i scisla o tym nalezy pamietac. Obszar. D. x²+y²= 4 ,moje wpisy z dnia 25 czerwiec uwazam za poprawne.

Michalina: a kto pisze że punkt jest obszarem. Napisane jest wyraźnie że ograniczone obszarami a te obszary zawierają punkt

Leszek: Na Pani rysunku z godziny 16,30 p K nie nalezy do obszaru calkowania ,bo obszar calkowanie jest plaski a nie platem powierzchni bo wowczas inaczej powinna byc tresc zadania.

piotr: ∫−22 ∫−√4−x2√4−x2 ∫−√−x2−y2+8√x2+y2 z dz dy dx = −8π

Leszek: Jezeli to jest bryla ,a tak sie wydaje to wynik dla objetosci musi byc dodatni.

Michalina: przecież to jest wyraźnie obszar stożka z sferycznym dnem zawierającym niebieski punkt. Na czerwono zaznaczyłem promień stożka

Michalina: to nie jest objętość tylko całka ∫∫∫z

piotr: całkujemy po obszarze znajdującym się poniżej płaszczyzny XY, a więc z<0 stąd wynik ujemny

bezendu: Qulka co to za zbiór ? Możesz podać link ?