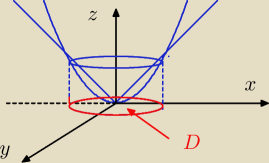
objętość ograniczona krzywymi Michalina: objętość ograniczona krzywymi z=x²+y² z²=x²+y² rozumiem że jest to paraboloida na zewnątrz ograniczona stożkiem po wewnątrz. Należy dobrać przedziały całkowania dla r, z i ∅ ∅=0, 2π co z r i z? całka będzie wyglądać tak: ∭r dzd∅dr ?

Leszek: ∫ ∫ dxdy[√x²+y²−(x²+y²)] D zastosuj współrzędne biegunowe D : r ∊ <0;1> φ ∊<0 ; 2π>

Michalina: skąd r od 0 do 1?

Leszek: popatrz na rysunek w płaszczyznie XZ ; z=|x| i z= x² => x=0 lub x=1 lub x=−1 obszar D : x² +y² = 1

piotr:

	π
V= ∫02π ∫01 (r2−r3) dr dθ =
	6

piotr:

	π
∫−11 ∫−√1−x2√1−x2 ∫x2+y2√x2+y2 1 dz dy dx =
	6

Michalina: @piotr skąd ci się wzięło pod całką r²−r³? Powinno być r−r³ i wtedy wychodzi π/2

Michalina: sorry racja powinno być r²−r³ po jakobian nie wziąłem za nawias