l. zespolone bartman23: Proszę podać (w postaci trygonometrycznej) wartości wszystkich, istotnie rożnych liczb zespolonych z spełniających równanie: z³ = −1 + i

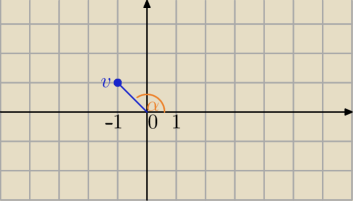
Mila: z=³√−1+i v=−1+i |−1+i|=√2

	3π
α=
	4

	3π   +2kπ 4		3π   +2kπ 4
zk=6√2*(cos		+i sin		), k=0,1,2
	3		3

	π		π		√2		√2
z0=6√2*(cos		+i sin		)=6√2*(		+i sin		)
	4		4		2		2

licz dalej sam

bartman23: dlaczego dla k = 0, 1, 2?

Mila: Takie są zasady. Poczytaj o wzorze de Moivre'a. Masz otrzymać 3 pierwiastki.

bartman23: dzięki